Chapter 6
Collisions of Charged Particles
The interactions of a moving charged particle with any surrounding matter are
governed by the properties of collisions. We will usually call the
incident particle the "projectile" and the components of the matter
with which it is interacting the "target-particles" or just the
"targets". The simplest situation one
might imagine is that the matter consisted of free charged particles,
electrons and nuclei. This is exactly the situation that applies if
the matter with which the particle is interacting is a plasma. It
might be thought that in this case, the mutual interaction of the
target-particles themselves could be ignored, and the collisions
treated as if they were all simple two-body collisions. This is not
quite true because of the long-range nature of the electromagnetic
force, as we shall see, but it is possible, nevertheless, to treat the
collisions as two-body, but correct for the influence of the other
target particles in this process.
In interactions with the atoms of solids, liquids or (neutral) gases,
the fact that the target electrons are bound to the nuclei of their
atom is obviously, in the end, important to the interaction
processes. The atoms themselves can usually be treated ignoring the
interactions between them, at least for projectiles with substantial
kinetic energy. The simplest approximate analysis goes further, and
starts from the highly simplified view that the electrons can be
treated initially ignoring the force binding them to atoms. The
corrections to this approach are naturally substantial, and the
treatment cannot always yield accurate results. Nevertheless it
represents a kind of baseline that more accurate calculations and
measurements can be compared with.
The nuclei of the target are important in collisions with
plasmas. However, in interactions with neutral atoms, direct
electromagnetic interaction with the nucleus requires the projectile
to penetrate the shielding of the orbiting electrons in the atom.
Only particles with very high momentum can do that. Therefore the
electrons of the target are usually the most important to consider,
and tend to dominate the energy loss.
The topic of atomic collisions is an immense and complex one, in which
quantum mechanics naturally plays a crucial role. It would take us far
beyond the present intention to attempt a proper introduction to this
topic. Two simplifying factors enable us, nevertheless, to develop
this aspect of electromagnetic interactions in enough detail for many
practical purposes. The first factor is that the details of atomic
structure become far less influential in collisions at energies
much higher than the binding energies of atoms (which is about ten electron
volts or so). The second is that even when quantum effects are
important in the collisions, approximate formulas with wide
applicability, but ignoring the details of particular atomic species,
can be obtained by semi-classical arguments. The quantum corrections
are then applied in a way that seems somewhat ad hoc, but often
represents the way the earliest calculations were done, and gives
simple analytic formulas.
6.1 Elastic Collisions
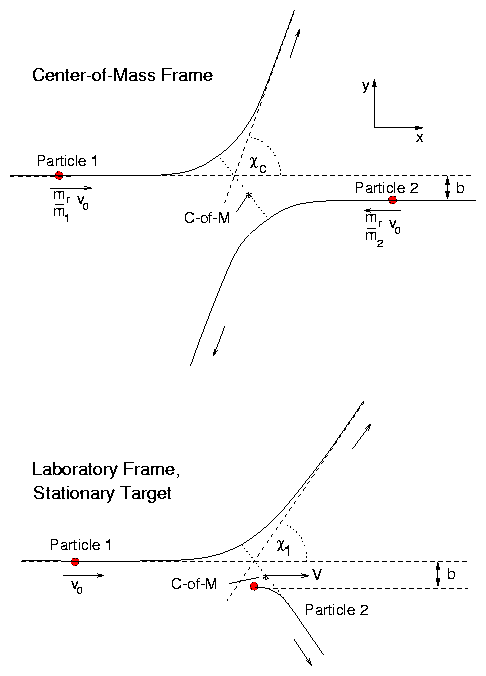
6.1.1 Reference Frames and Collision Angles
Consider an idealized non-relativistic collision of two interacting
particles, subscripts 1 and 2, with positions r1,2 and
velocities v1,2, which are not acted on by any forces other
than their mutual interactions and which experience no changes in internal
energy, so the collision is elastic. Their total (combined) momentum,
m1v1 + m2v2, is constant, so that their center-of-mass,
moves at a
constant velocity, the center-of-mass velocity:
It is helpful also to introduce the notation
for what is called the "reduced mass". In terms of
this quantity and the relative position vector r ≡ r1 −r2, the positions of the particles can be written:
|
r1 = R + |
mr
m1
|
r r2 = R − |
mr
m2
|
r , |
| (6.4) |
and their velocities:
|
v1 = V + |
mr
m1
|
v v2 = V − |
mr
m2
|
v , |
| (6.5) |
where v ≡ · r is the relative velocity.
Some of our calculations need to be done in the center-of-mass frame
of reference, in which R is stationary. Others need to be done in
the lab frame or other frames of reference, for example in which one
or other of the particles is initially stationary. The angles of
vectors in these frames are important. The directions of all position
vectors and of all velocity differences are the same in all
inertial frames. However the directions of velocities are not
the same in different frames.
For example, consider a collision illustrated in Fig
6.1. Collisions can be considered in a single
plane-of-scattering which is perpendicular to the angular momentum of
the system, itself a constant. The angle of scattering, which we
denote χ is just the angle between the initial direction
of the relative velocity v and its final direction,
v′. This angle is different in different reference frames. Call
the angle in the center-of-mass frame χc. By conservation of
energy, the final relative velocity v′ has absolute magnitude
equal to that of the initial relative velocity, v0. So the final
velocity can be written in component form, in the center of mass
frame, as
where we have chosen the initial relative velocity direction
for the x-axis.
Figure 6.1: Collisions in center-of-mass and laboratory frames.
Substituting into eq(6.5) we find the final velocities in the lab
frame to be given by
| |
|
|
| ⎛
⎝
|
mr
m1
|
v0 cosχc + V, |
mr
m1
|
v0sinχc | ⎞
⎠
|
, |
| | (6.7) |
| |
|
| ⎛
⎝
|
− |
mr
m2
|
v0 cosχc + V, − |
mr
m2
|
v0sinχc | ⎞
⎠
|
. |
| | (6.8) |
|
The angle in the lab frame of the final velocity of
particle 1 to its initial velocity (which is in the x-direction) ,
χ1 say, is then just given by the ratio of the components of the
final velocity,
|
cotχ1 = |
|
= cotχc + |
V
v0
|
|
m1
mr
|
cscχc . |
| (6.9) |
For the specific case when particle 2 is a stationary target,
with initial lab-frame velocity zero, the center-of-mass velocity is
V = m1v0/(m1+m2) = (mr/m2) v0 and so
|
cotχ1 = cotχc + |
m1
m2
|
cscχc . |
| (6.10) |
We often want to know how much energy or momentum is transferred from
an incident projectile, (particle 1) to an initially stationary
target (particle 2). Clearly from eq(6.8) we can obtain
these quantities in terms of the scattering angle χc. So, the
change in the x-momentum of particle 1 is simply
|
m1 | ⎛
⎝
|
mr
m1
|
v0cosχc+V | ⎞
⎠
|
− mv0 = mr v0 | ⎛
⎝
|
cosχc+ |
m1
m2
| ⎞
⎠
|
|
| (6.11) |
and the final recoil energy of particle 2 (which is the energy lost by
particle 1) is
| |
Q ≡ |
1
2
|
m2 | ⎡
⎣
| ⎛
⎝
|
− |
mr
m2
|
v0 cosχc + V | ⎞
⎠
|
2
|
+ | ⎛
⎝
|
− |
mr
m2
|
v0sinχc | ⎞
⎠
|
2
| ⎤
⎦
|
|
|
|
| |
| |
|
1
2
|
m2 | ⎛
⎝
|
mr
m2
|
v0 | ⎞
⎠
|
2
|
[ (− cosχc +1 )2 + sin2χc] |
|
|
| |
| |
|
1
2
|
|
mr2
m2
|
v02 2(1 − cosχc) |
|
|
|
1
2
|
|
mr2
m2
|
v02 4 sin2( |
χc
2
|
) . |
| | (6.12) |
|
Notice that the maximum possible energy transfer, which occurs when
χc=180°, is
|
Qmax = |
4 mr2
m1m2
|
[1/2]m1v02 . |
| (6.13) |
All of these relations are completely independent of the nature of the
interaction between the particles, since we have invoked only
conservation of momentum and energy.
Impact Parameter and Cross-section
By definition, the cross-section, σ, for any specified
collision process, when a particle is passing though a density n2
of targets, is that quantity which makes the number of such
collisions per unit path length equal to n2σ.6 Sometimes a continuum
of types of collision is under consideration. For example we can
consider collisions giving rise to different scattering angles
(χ) to be distinct. In that case, we speak in terms of
differential cross-sections, and define the differential
cross-section [(dσ)/(dχ)] (for example) as being that
quantity such that the number of collisions within an angle element
dχ per unit path length is
Sometimes other authors use different notation for the differential
cross-section, for example σ(χ). However, our notation, with
which we are familiar from calculus, is highly suggestive and the
cross-sections obey natural rules for differentials implied by the
notation.
For classical collisions, the impact parameter, b, shown in
Fig 6.1, is a convenient parameter by which to
characterize the collision. It is the distance of closest approach
that would occur for the colliding particles if they just followed
their initial straight-line trajectories. Alternatively, the impact
parameter can be considered to be a measure of the angular momentum of
the system in the center-of-mass frame, which is mr v0 b.
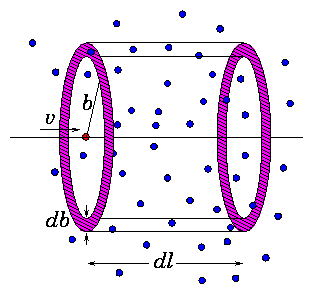
Figure 6.2: Differential volume for counting the number of collisions in
length dl with impact parameter b.
The differential cross-section with respect to the impact parameter is
defined purely by geometry. As illustrated in Fig 6.2, one
can think of the projectile (particle 1) as dragging along with itself
an anulus of radius b and thickness db as it moves along a
distance dl of its path length. This anulus drags out a volume
dl2πb db, and the number of targets that are in this volume,
and hence have been encountered in the impact parameter element db
at b in this path-length is n2 dl2πb db. Consequently,
from our definition, the differential cross-section for scattering at
impact parameter b is
Notice that the integral of this quantity over
all impact parameters (i.e. 0 < b < ∞) will certainly diverge,
because it considers the projectile to be colliding with all the
target particles it passes, no matter how far away they are. Therefore
the total number of "collisions" of all possible types, per unit
length in an infinite target medium is infinite. This mathematical
singularity in the "total cross-section" points out the need to
define more closely what constitutes a collision, and alerts us to the
fact that for collisions governed by interactions of infinite range,
such as the forces between charged particles, we shall have to define
our collisions in such a way as to account for some effective
termination of the impact-parameter integration.7 This termination, which is often
expressed approximately as a cut off of the impact parameter
integration at a maximum bmax, will be governed by
consideration of the particle parameter whose change due to collisions
we are trying to calculate. For example, the momentum or energy change
in the collision may become negligible for b > bmax.
There is usually a one-to-one relationship
between the impact parameter and the angle of scattering and hence
with the energy transfer, Q, given by
eq(6.12). Consequently the differential cross-section with
respect to energy transfer, scattering angle and impact parameter are
all related thus:
|
|
dσ
dQ
|
= |
dσ
dχc
|
| ⎢
⎢
|
dχc
dQ
| ⎢
⎢
|
= |
dσ
db
|
| ⎢
⎢
|
db
dχc
| ⎢
⎢
|
| ⎢
⎢
|
dχc
dQ
| ⎢
⎢
|
|
| (6.15) |
If we are concerned with a quantity such as the energy of the
projectile, which is changing because of collisions, and the change in
each collision is an amount Q(b) that depends on the impact
parameter, then the total rate of change per unit length due
to all possible types of collisions is obtained as
|
n2 | ⌠
⌡
|
Q dσ = n2 | ⌠
⌡
|
Q 2πb db |
| (6.16) |
6.1.2 Classical Coulomb Collisions
The exact relationship between the impact parameter, b, and the
scattering angle is determined by the force field existing between the
colliding particles. For electromagnetic interactions of charged
particles, the fundamental force is the Coulomb interaction between
the forces, an inverse square law. As Isaac Newton showed, the orbit
of a particle moving under an inverse square law force is a conic
section; that is, an ellipse for closed orbits or a hyperbola for the
open orbits relevant to collisions.
Elementary analysis shows that the resulting scattering angle χc
for a collision with impact parameter b is given by
where, for particles of charge q1 and q2 and initial collision
velocity v0 the quantity b90 is given by
|
b90 ≡ |
q1q2
4πϵ0
|
|
1
mr v02
|
. |
| (6.18) |
Clearly from eq(6.17), b90 is the impact parameter at
which the scattering angle in the center of mass frame is
90°. Trignometric identities allow us to deduce immediately from
eq(6.17) that
|
sin2(χc/2) = |
1
1+(b/b90)2
|
and |
db
dχc
|
= − |
b90
2
|
csc2(χc/2) . |
| (6.19) |
So that the energy transfer in a collision (see eq(6.12)) is
|
Q = |
1
2
|
|
mr2
m2
|
v02 4 |
1
1+(b/b90)2
|
|
| (6.20) |
and the rate of transfer of energy per unit length for a particle
of energy K ≡ [1/2]m1v02 colliding with stationary targets is
|
− |
dK
dl
|
= n2 |
m1v02
2
|
|
4mr2
m1m2
|
| ⌠
⌡
|
|
2πb db
1+(b/b90)2
|
= n2 K |
4mr2
m1m2
|
πb902ln[1+(bmax/b90)2] , |
| (6.21) |
where the upper limit of the b-integration, bmax, which
prevents the integral diverging, will be discussed in a moment. One
way to think of this equation is to regard the quantity
πb902[(4mr2)/(m1m2)] ln[1+(bmax/b90)2]
as an effective collision cross-section for total energy loss. When
multiplied by the density n2 of targets it gives the inverse scale-length
for energy loss, dlnK/dl.
Figure 6.3:
Scattering angle and impact
parameter shown schematically for different Coulomb collisions.
6.2 Inelastic Collisions
The effects that give rise to the cut-off of the Coulomb logarithm are
primarily associated with the presence of other particles and forces
in the system. If the target particles experience the force-field of
another nearby particle, such as will be the case if the targets are
electrons bound to the nuclei to form the atoms of a target material,
then the dynamics of their binding gives rise to a cut-off. One way to
think of this effect is to regard the electrons as behaving as if they
were free only in collisions in which the energy transfer from the
projectile is larger than their binding energy in the atom. Distant,
small angle, collisions transfer less energy. A cut-off
bmax should be applied at that impact parameter where the
energy transfer is equal to approximately the binding energy.
Alternatively, and more physically, one can regard these collisions as
being with a composite target system, the atom, in which there is a transfer
of energy inelastically to the system, the energy being partially
taken up in the ionization or excitation energy of the atom.
Clearly, a fully rigorous calculation of such collisions
requires the quantum structure of the atom to be considered, and so is
intrinsically quantum-mechanical. Nevertheless, semi-classical
calculations, taking quantum effects into account in a somewhat ad hoc
manner, give substantial insight into the governing principles and, in
fact, are able to give quantitatively correct forms for the
cross-sections and energy loss.
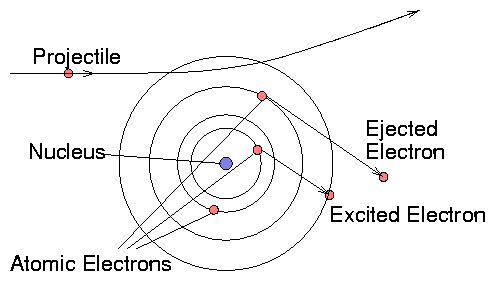
Figure 6.4:
Collisions with an atomic
system can excite or eject electrons from the atom.
6.2.1 Energy transfer to an oscillating particle
An approach to the problem of collisions with bound particles that
can be treated classically, and becomes the basis for a quantum
description, is to approximate the system as a charge bound in a
simple harmonic potential well. Because we are mostly interested in
large impact parameters, we regard the electric field of the
projectile as uniform at the atom and then ask the question, in the
encounter of the projectile with this oscillating electron, how much
energy does the oscillator gain as a result of the fluctuating
electric field of the passing projectile.
So consider a simple oscillating particle in a uniform electric field,
E(t). Its position x is governed by the equation
We solve this equation in the time range (t1,t2), with some
assumed initial condition at t1 so as to determine the energy
gained by the particle at time t2. This solution is readily
obtained using what is called the "one-sided Green function" as
follows. The solutions to the homogeneous problem (the equation with
zero right hand side) are sinωt and cosωt. The
Green function is constructed as
|
H(t,τ) = (sinωt cosωτ− cosωt sinωτ)/ω |
| (6.23) |
and the general solution is then
|
x(t) = A sinωt + B cosωt + |
t
⌠
⌡
t1
|
H(t,τ) |
q
m
|
E(τ) dτ , |
| (6.24) |
where A and B are constants determined by the initial
conditions.
For simplicity consider the initial conditions to be that the
oscillator is at rest: A=B=0.
Then at time t2 the solution may be written
|
|
ωm
q
|
x(t2) = sinωt2 |
t2
⌠
⌡
t1
|
cosωτE(τ)dτ− cosωt2 |
t2
⌠
⌡
t1
|
sinωτE(τ)dτ . |
| (6.25) |
When this expression is differentiated, the terms arising from
the differentials of the limits cancel and we get
|
|
ωm
q
|
|
⋅
x
|
(t2) = ωcosωt2 |
t2
⌠
⌡
t1
|
cosωτE(τ)dτ+ ωsinωt2 |
t2
⌠
⌡
t1
|
sinωτE(τ)dτ . |
| (6.26) |
So the total (kinetic plus potential) energy in the oscillator can
then rapidly be evaluated as
| |
|
|
|
q2
2m
|
| ⎡
⎣
| ⎛
⎝
|
t2
⌠
⌡
t1
|
cosωτE(τ)dτ | ⎞
⎠
|
2
|
+ | ⎛
⎝
|
t2
⌠
⌡
t1
|
sinωτE(τ)dτ | ⎞
⎠
|
2
| ⎤
⎦
|
|
| |
| |
|
| | (6.27) |
|
with the Fourier transform of the electric field written
|
E(ω) = | ⌠
⌡
|
exp(iωτ) E(τ) dτ . |
| (6.28) |
We did this integration over a finite time, which avoids some
mathematical difficulties, but we can now readily let
t1 → −∞ and t2 → ∞ and obtain the full domain
Fourier integral. We have obtained the important general result that
the energy transferred to a harmonic oscillator is proportional to the
Fourier transform of the electric field evaluated at the resonant
frequency of the oscillator, eq(6.27).
6.2.2 Straight-Line Collision
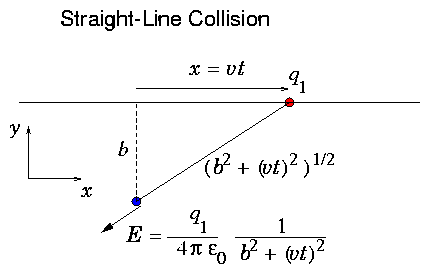
Figure 6.5: The approximation of a straight orbit gives a simple
expression for the electric field as a function of time.
We are interested mostly in small-angle collisions, because, as we
previously noted, they dominate the behavior, especially at the
cut-off, bmax. We approximate the orbit of the projectile
in this case as a straight-line. Then, as illustrated in Fig
6.5, the electric field at the atom is
just that due to a charge moving past at an impact parameter b and a
constant speed. For a non-relativistic speed v the components of the
electric field as a function of time are then
|
Ex(t) = |
−q1
4πϵ0
|
|
v t
(b2+ v2t2)3/2
|
and Ey(t) = |
−q1
4πϵ0
|
|
b
(b2+ v2t2)3/2
|
. |
| (6.29) |
the relativistic forms are qualitatively similar, and were calculated
previously in section 4.2, see eq(4.39)
|
Ex(t) = |
−q1
4πϵ0
|
|
γv t
(b2+ γ2 v2t2)3/2
|
and Ey(t) = |
−q1
4πϵ0
|
|
γb
(b2+ γ2 v2t2)3/2
|
, |
| (6.30) |
where γ is the relativistic factor (1−v2/c2)−1/2.
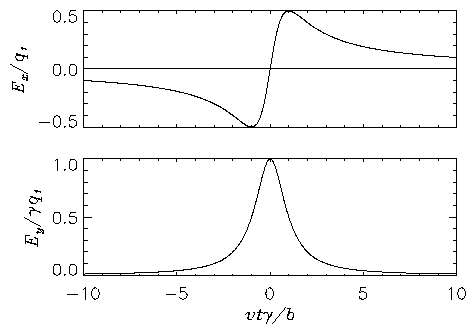
The field components are plotted as a function of time in Fig 6.6.
Figure 6.6: The electric field components in a straight-line collision.
Clearly, by inspection of Fig 6.6, and eq(6.28) there
will be a qualitative change in the behaviour of the Fourier transform
of E(t) and hence the energy transfer for ωb/γv >> 1
compared with ωb/γv << 1. The characteristic time
duration of the collision is ∼ b/γv. If this is much shorter
than the characteristic oscillator time, 1/ω, we can take
ω ≈ 0 and obtain by elementary integration
Because Ex(t) is antisymmetric, Ex(ω) = 0 in this small
impact parameter limit. In the opposite limit, that is for collisions
in which b is so large that ωb/γv >> 1, E(ω)
will be small because in eq(6.28) there are many oscillations of
the factor exp(−iωt) within the smooth variation of
E(t). Thus we see that in collisions with a simple harmonic
oscillator of frequency ω, there is a natural cut-off to the
energy transfer at a maximum impact parameter
Substituting eq(6.31) into eq(6.27), and
restoring our notation of subscript 2 for the target and subscript
0 for the incident velocity, we obtain
the energy transfer in a straight-line collision as
|
Q(b) = |
q12q22
(4πϵ0)2
|
|
2
m2 v02 b2
|
= |
1
2
|
|
mr2
m2
|
v02 4 | ⎛
⎝
|
b90
b
| ⎞
⎠
|
2
|
|
| (6.33) |
Notice that this is essentially the same expression as in
eq(6.20) for the energy transfer to a free electron,
except that the lower impact-parameter cut-off is not present here
because of the assumption of a straight-line orbit for the projectile,
which is unjustified at small impact parameters. The rate of energy
loss is then obtained, as before, by integration over impact
parameters from the minimum to the maximum corresponding to the limits
of applicability of eq(6.31)
|
− |
dK
dl
|
= n2 K πb902 |
mr2
m1m2
|
8ln | ⎢
⎢
|
bmax
bmin
| ⎢
⎢
|
= n2 | ⎛
⎝
|
q1q2
4πϵ0
| ⎞
⎠
|
2
|
|
4π
m2 v02
|
ln | ⎢
⎢
|
γv0
ωb90
| ⎢
⎢
|
. |
| (6.34) |
6.2.3 Classical Energy Loss Rate Formula
One final consideration is needed before we have an energy loss
formula useful for practical purposes. We have to have some way of
applying the idealized harmonic oscillator calculation to actual
atoms. An atom in general has a number Z, say, of electrons bound to
the nucleus. Each electron may act as a target oscillator for energy
transfer, and actually each electron may act as one of an infinite set
of oscillators, corresponding to each of its possible quantum
transitions. Energy transitions of magnitude Ei correspond to
oscillators of frequency ωi = Ei/ħ, of course. To the
ith transition may be assigned an oscillator strength, fi,
defined as the ratio of the actual rate of energy absorption by that
transition to that of a corresponding harmonic
oscillator. The semi-classical argument is then that each electron
spends some fraction of its time behaving as if it were each of the
possible oscillators, and consequently ∑fi = Z. There is
a more rigorous theorem in quantum physics called the (Thomas-Reiche-Kuhn)
f-sum rule which states that the sum of all possible transition
oscillator strengths from a specific level is equal to the number of
electrons in the level. If this were applied blindly to all the
electrons of the atom, it would give the same equation.
To obtain the total energy loss rate arising from collisions with
a density of atoms na, whose atomic number is Z, we add up
the contributions from all the possible transitions, weighted by the
oscillator strength of that transition. Thus we obtain for the
logarithmic term:
|
|
∑
i
|
fi ln | ⎢
⎢
|
γv0
ωi b90
| ⎢
⎢
|
= Zln | ⎢
⎢
|
γv0
b90
| ⎢
⎢
|
− |
∑
| filnωi = Z ln | ⎢
⎢
|
γv0
〈ω〉b90
| ⎢
⎢
|
, |
| (6.35) |
where we have defined
a kind of average oscillator frequency 〈ω〉 by the equation
The total classical energy loss rate is then
|
|
dK
dl
|
= na | ⎛
⎝
|
q1e
4πϵ0
| ⎞
⎠
|
2
|
|
4π
mev02
|
ZlnΛ , |
| (6.37) |
where we have substituted electron charge and mass for particle 2, and
for brevity denoted the argument of the logarithm by
Actually, it turns out to be possible to evaluate the Fourier
transforms of the relativistic fields in eq(6.30) in closed
form and carry through the integration of the modified Bessel
functions thus obtained [see Jackson]. When that
is done, two very small corrections to our formula appear. The
argument of the logarithm is multiplied by the factor 1.123 and an
additional relativistic term is added, equivalent to the replacement
|
lnΛ → ln | ⎢
⎢
|
1.123 γv0
〈ω〉b90
| ⎢
⎢
|
− |
v02
2c2
|
. |
| (6.39) |
Neither of these corrections is quantitatively significant. The
result was first obtained by Bohr in 1913, prior to the development of
quantum mechanics. It is hardly complete as it stands, since the
average 〈ω〉 has to be estimated. However, because
〈ω〉 appears only in the logarithm, even a rough
estimate, for example setting ħ〈ω〉 equal to the
atom's ionization potential, will give a useful quantitative formula
for the energy loss.
6.2.4 Quantum effects on close collisions
For the classical minimum impact parameter b90 to be applicable
requires that the particles of the collision behave as point particles
down to that impact parameter. However, quantum mechanics teaches us
that particles do not behave like perfect points. The Heizenberg
uncertainty principle states that the particle is localized only
within a position uncertainty ∆x if its momentum uncertainty
is ∆p such that ∆x ∆p ≈ ħ. Alternatively one can say that a particle with momentum p = γm v behaves like a wave with wave-vector k = p/ħ. Or again, one
can say that orbital angular momentum is quantized in indivisible units of
ħ. All of these are ways of indicating that in collisions the
effective position of a particle is spread out over a distance of
order ħ/p. Consequently, quantum effects prevent us from
extending the classical integration over impact parameters below a
value of
(using the reduced mass as the appropriate one for quantum cut-off momentum).
The classical b90 lower impact parameter cut-off will be
applicable only if
|
|
b90
bq
|
≈ |
q1q2
4πϵ0 ħ v
|
= |
q1q2
e2
|
α |
c
v
|
> 1 , |
| (6.41) |
where α is the fine structure constant, approximately 1/137,
This criterion is a requirement that the collision velocity
with electron targets should be less than Z1 c/ 137.
In practice this means that electrons with energy greater than 13.6
eV, protons with energy greater than 25 keV, or alpha particles with
energy greater than 400 keV will not be appropriately treated
using the classical lower impact parameter cut off. Instead, an
approximation to the quantum-mechanical result may be obtained by simply
cutting off the impact parameter integration at bq rather than
b90. If we choose8 bq = ħ/2γme v,
then in collisions of heavy particles with atoms, for which mr = me,
|
ln | ⎢
⎢
|
bmax
bmin
| ⎢
⎢
|
= ln | ⎢
⎢
|
2γ2me v02
ħ〈ω〉
| ⎢
⎢
|
. |
| (6.42) |
This value is then consistent with that obtained for the relativistic
case using a quantum scattering treatment and the first Born
approximation, by Bethe (1930),
|
− |
dK
dl
|
= na | ⎛
⎝
|
q1e
4πϵ0
| ⎞
⎠
|
2
|
|
4π
mev02
|
Z | ⎛
⎝
|
ln | ⎢
⎢
|
2γ2me v02
ħ〈ω〉
| ⎢
⎢
|
− |
v02
c2
| ⎞
⎠
|
, |
| (6.43) |
where again the final term, v02/c2, which we have not derived, is at most a
small correction.
If the projectile is an electron or positron, then the quantum cut-off
must be estimated in the center-of-mass frame, and the expression
becomes
|
− |
dK
dl
|
= na | ⎛
⎝
|
e2
4πϵ0
| ⎞
⎠
|
2
|
|
4π
mev02
|
Z | ⎛
⎝
|
ln | ⎢
⎢
| ⎛
⎝
|
γ+1
2
| ⎞
⎠
|
1/2
|
|
(γ−1)me c2
ħ〈ω〉
| ⎢
⎢
|
− |
v02
2c2
| ⎞
⎠
|
. |
| (6.44) |
6.2.5 Values of the Stopping Power
We have so far left open the question of what value to take for
ħ〈ω〉. Bloch (1933) showed from an analysis of
the Thomas-Fermi model of the electron charge distribution in an atom
that one would expect that ħ〈ω〉 ∝ Z. In
recognition of the work of Bethe and Bloch, eq 6.43
is often referred to as the Bethe-Bloch formula. The formula is often
written as
|
− |
dK
dl
|
= na | ⎛
⎝
|
q1e
4πϵ0
| ⎞
⎠
|
2
|
|
4π
mev02
|
B , |
| (6.45) |
with the quantity B, called the "atomic stopping number",
corresponding to the factor
|
Z | ⎛
⎝
|
ln | ⎢
⎢
|
2γ2me v02
ħ〈ω〉
| ⎢
⎢
|
− |
v02
c2
| ⎞
⎠
|
. |
|
Also
B/Z is then called the "stopping power" per (atomic) electron,
recognizing that an atom has Z electrons. The stopping
power is determined from experiments, and the appropriate value to use
for ħ〈ω〉 is determined from those
measurements.
A complication that we have not discussed arises because
our treatment has assumed that the orbital velocity of the electrons
in the atom can be ignored relative to the velocity of the incident
particle. This is not the case when dealing with the inner shell
electrons of high-Z atoms or very low incident-energy projectiles. Then
a reduction in the stopping number occurs because (for example) the
(innermost) K-shell electrons are ineffective in removing the
projectile's energy. This effect is
numerically compensated by
substracting a correction term CK so that
|
B = Z | ⎛
⎝
|
ln | ⎢
⎢
|
2γ2me v02
ħ〈ω〉
| ⎢
⎢
|
− |
v02
c2
| ⎞
⎠
|
− CK . |
| (6.46) |
In this form, the value of ħ〈ω〉 is empirically
determined to be about 11.5×Z eV, and CK is a function of
the quantity ξ ≡ (c2/v02)(Z−0.3)2 α2 (which
represents the squared ratio of the K-shell velocity to the
projectile velocity). A simple approximate form for CK is
correct to within 10% from ξ = 0 to ξ = 2.
It tends to zero at high projectile energy and peaks at about unity
at low velocity, where ξ ≈ 1.
These and many other details have been reviewed by Evans (1955).
6.2.6 Effects of surrounding particles on distant collisions
Let us return now to our primitive energy loss rate calculation, eq
6.34 which may be considered in the form
|
|
dK
dl
|
= n2 | ⎛
⎝
|
q1q2
4πϵ0
| ⎞
⎠
|
2
|
|
4π
m2v02
|
ln | ⎢
⎢
|
bmax
bmin
| ⎢
⎢
|
. |
| (6.48) |
In the preceding sections we have been discussing appropriate choices
of bmin based either on the classical effects of large
scattering angles (giving b90) or on quantum-mechanical effects
of the de Broglie wave-length of the projectile/target combination. We
also discussed the appropriate bmax based on the effects
of the binding of electron targets to their nuclei. However, another
effect can sometimes be more important than the atomic binding
structure in determining bmax, namely the influence of
surrounding particles.
We have tacitly assumed so far that the interaction of the projectile
and any specific target can be treated ignoring the effects of
the other targets in the vicinity. We have calculated the
projectile/target interaction in isolation and then presumed that we
can add up the effects of all the different targets via a simple
impact-parameter integration. This may not be the case. For example,
it definitely is not the case when the electrons of the target are
unbound; or in other words for a plasma target. In that case
there is no intrinsic cut-off to the the collision integral arising
from the oscillator effects introduced in section 6.2.1 and
the effect of the nearby particles essentially always determines
bmax. Even in collisions with atomic matter, especially
for relativistic electrons, the effect of nearby particles can
significantly lower the energy transfer rate. In the atomic collision
context the corrections are often referred to as the "density
effect" because they are most significant for high-density matter.
It is still the case that transfer of energy to the target arises from
the electric field produced by the incident projectile. However, what
we need to do is to account for the influence of the other particles
in the target medium on the electric field that the projectile
produces at a specific target. Expressed in this way, it is
immediately clear that what we need is to take account of the
dielectric properties of the target medium. The individual particles
of the medium respond to the influence of charge (the projectile in
this case) so as to alter the electric field in the medium from what
it would otherwise have been. This is exactly what we mean by the
dielectric response of the medium.
Of course, though, it is not the steady-state dielectric response that
we require but the response at the high frequencies of interest in the
collisions. Moreover, when we think about a target medium consisting of
a density of idealized oscillators, as we did before, it is the
properties of those oscillators themselves that determines the
dielectric response at frequencies close to their resonant
frequencies. Thus the dielectric response and the energy-loss collisional
response are not two separate properties of the medium; they are
intimately connected.
The idealized oscillator model can be generalized to discuss a medium
with any relative dielectric permittivity ϵ(ω) having a resonant
form (ϵ−1 ∝ (ω− ωi)−1), and an expression for the
rate of loss of energy of an incident projectile to this resonance can
then be obtained. Fermi (1940) first gave the following formula, which
would take us too long to rederive, for the
energy loss attributable to collisions with impact parameter greater
than a as
|
|
dK
dl
| ⎢
⎢
|
b > a
|
= |
2
π
|
|
q12
4πϵ0 v02
|
ℜ | ⌠
⌡
|
∞
0
|
i s* K1(s*) K0(s) | ⎛
⎝
|
1
ϵ(ω)
|
− β2 | ⎞
⎠
|
dω , |
| (6.49) |
where ℜ denotes real part, β = v0/c, K1 and K2
are modified Bessel functions, and their argument is s such that
|
s2 ≡ |
a2ω2
v02
|
[1−β2ϵ(ω)] . |
| (6.50) |
It can be shown, but not trivially, [Jackson] that this dK/dl
reduces to the the Bohr expression (eq 6.39) if the
β2ϵ(ω) term in s is neglected.
Rather than pursue the topic for the atomic case, let us consider
a simple argument for a plasma. The dielectric constant for a
(magnetic field-free) plasma at high frequency is
where
is called the plasma frequency. Therefore when the field frequency of
interest is less than ωp the dielectric constant is negative
and wave electric fields no longer propagate in the medium; instead
they decay exponentially with distance from their source. In collisions,
as we have seen before, the frequency of the interaction electric
field is approximately v0/b. Therefore, for impact parameter, b,
greater than v0/ωp we would expect that the effectiveness of
the collisions would fall off because of the dielectric
effects. Applying this value for bmax we obtain an energy
loss rate expression corresponding to eq 6.37 as
|
|
dK
dl
|
= ne | ⎛
⎝
|
q1e
4πϵ0
| ⎞
⎠
|
2
|
|
4π
mev02
|
lnΛ = |
q12
4πϵ0
|
|
ωp2
v02
|
lnΛ |
| (6.52) |
but with Λ given approximately by
What we have done, in effect then, is to replace the value
bmax = γv0 /〈ω〉 in
the definition of Λ, eq (6.38) with
The factor by which the logarithmic argument Λ of the
Bethe-Bloch formula is
multiplied is therefore γωp/〈ω〉. But the density effect can only lower the
absorption rate so we should more properly have used bmax = min( v0/ωp, γv0/〈ω〉). The electrons
behave as if they are free when ω > ωij ∼ 〈ω〉. Hence plasma-like, i.e. free-electron,
behaviour occurs only when ωp > 〈ω〉, which is
when the plasma expression for bmax applies, because it is
the smaller.
A rough estimate of the ratio of ωp/〈ω〉 may
be obtained by taking the density of atoms in a solid to be about
1030 m−3, and the electron density to be Z times that. Then
For medium weight solid elements, ħ〈ω〉 ∼ 11Z eV so we expect the plasma effect to be slightly noticeable
since on this basis ωp/〈ω〉 > 1. The question
is a little more complicated than this, though because not all the
electrons are going to behave as if free so we have somewhat over
estimated the density of the electrons that behave as if free. In
extreme relativistic cases, γ >> 1 the plasma (density) effect
will always dominate.
6.3 Angular Scattering from Nuclei
Up to this point we have been discussing the energy loss of the
projectile and have focussed on its interactions with electrons. This
focus on electron targets is entirely appropriate for calculating
energy loss because, as illustrated by eq (6.21) or
(6.34) the rate of energy loss is, classically, inversely
proportional to the mass of the target particle9. Therefore
the loss of energy is in fact predominantly to the light particles,
electrons, and this predominance depends only on the elementary
dynamics of collisions. However, in addition to losing energy, the
projectile also generally experiences angular scattering in the
direction of its velocity. If this angular scattering is our concern,
as it was in Rutherford's original experiments on the angular
scattering of alpha particles which established that the nucleus is
far smaller than the atom, then collisions with the heavy particles in
our scattering medium, the nuclei of the atoms or the ions of a
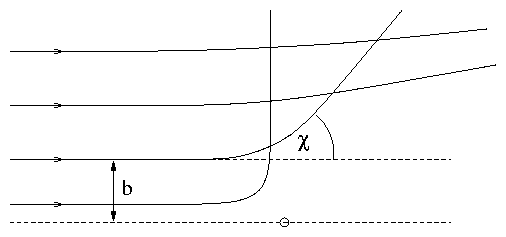
plasma, are important. This process, illustrated in Figure
6.7,
is often called "elastic
scattering", although the expression may be considered somewhat
misleading in that some energy is lost by the projectile in the
collision, and the process is no more elastic than a collision with
a free electron, for instance.
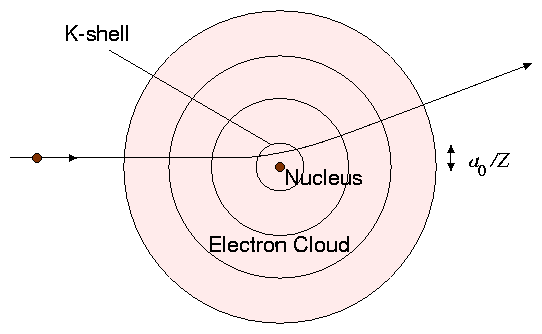
Figure 6.7:
Angular scattering from nuclei
occurs only if the impact parameter is less than the size of the electron
cloud.
|
|
dσ
dΩ
|
= |
b902
4 sin4 χc/2
|
. |
| (6.56) |
This formula may readily be derived from the considerations in section
6.1.1. It shows that the predominant scattering is through small
angles. Those small angles arise from large impact parameters. There
are some collisions, of course, which arise from small impact
parameters, close to b90, that give rise to large scattering
angles, but these are far fewer in number than the small-angle
collisions; so by the time the probability of scattering by a large
angle is significant, multiple scatterings by small angles will have
caused a kind of diffusion of the direction of the particles in
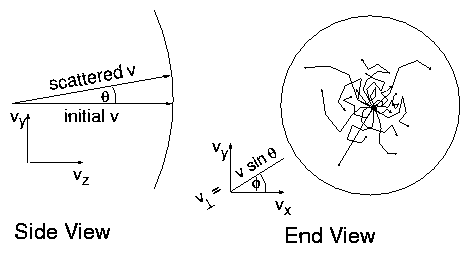
perpendicular velocity. Figure 6.8 illustrates an
idealized situation, in which the projectile loss of energy is taken
as zero, so its velocity vector has constant magnitude and moves on a
sphere. Taking the initial direction to be along the z-axis, each
small-angle collision causes a random step to be taken in the
(vx,vy) plane.
Figure 6.8: Multiple small-angle Coulomb collisions cause a diffusive
"random walk" of the angle of the projectile velocity, or
equivalently its perpendicular components.
Setting the large-angle collisions aside for a moment, we can treat
the total angular scattering experienced by a projectile passing
through a finite length of scattering path as the result of many small
scatterings each of which has random direction and magnitude, governed
by the fact that cot(χc/2) = b/b90 (eq
6.17). Although we cannot calculate for any individual
projectile what its final angle will be, we can treat the whole
process statistically, by presuming there to be many small-angle
scatterings. Actually, this calculation requires not the Rutherford
differential cross-section per unit solid-angle Ω, but the
differential cross-section per unit scattering angle χc,
|
|
dσ
dχc
|
= | ⎢
⎢
|
db
dχc
| ⎢
⎢
|
|
dσ
db
|
= |
b90
2
|
csc2(χc/2) 2 πb = πb902 csc2(χc/2)cot(χc/2) , |
| (6.57) |
which result is obtained immediately from our previous formulae.
The mean scattering angle experienced by the projectiles is
always zero, because there is equal probability of scattering at
negative and positive angles; the scattering is isotropic in the
(vx,vy) plane. The spread of scattering angles is quantified by
the mean square scattering angle, which is non-zero and can be
evaluated as follows. Succeeding collisions are statistically
independent of each other. The final value of vx is given by the
sum of the steps in vx at each of the individual
collisions. (Similarly for vy.) We therefore make use of the basic
statistical theorem that the variance (which is the mean-square value
for a zero-mean random variable) of the sum of independent random
variables is the sum of the variances. We perform this sum by dividing
the collisions into appropriate ranges of scattering angle dχc
and azimuthal angle dϕ. The number of steps per unit path length
belonging in these ranges is
and the change in vx that such collisions cause is
|
δvx = (mr/m1) v0 sinχc cosϕ . |
| (6.59) |
Here, the quantity (mr/m1)v0 is the initial (and final) speed of the
incident particle (1) in the center-of-mass frame.
Consequently, the total variance of vx per unit path length arising
from all possible types of collisions is
|
|
d〈vx2〉
dl
|
= | ⌠
⌡
|
(δvx)2 dN = | ⌠
⌡
|
| ⌠
⌡
|
n2 v02(mr/m1)2 sin2χc cos2ϕ |
dσ
dχc
|
dχc |
dϕ
2π
|
. |
| (6.60) |
Performing the integration over azimuthal angle, ϕ, and
substituting for the differential cross-section from eq (6.57)
we get
| |
|
|
|
1
2
|
n2 v02(mr/m1)2 | ⌠
⌡
|
sin2χc |
dσ
dχc
|
dχc |
| |
| |
|
|
1
2
|
n2 v02(mr/m1)2 πb902 | ⌠
⌡
|
sin2χccsc2(χc/2)cot(χc/2) dχc . |
| | (6.61) |
|
The final integral may be transformed using trignometric identities, becoming
|
| ⌠
⌡
|
sin2χccsc2(χc/2)cot(χc/2) dχc = 8 | ⌠
⌡
|
|
1
s
|
− s ds (s ≡ sinχc/2). |
| (6.62) |
The upper limit of the integral is s=1. The singularity of this
expression at zero lower limit of s shows again the now-familiar
need for a cut-off of the collision integral at large impact-parameter
(small χc or s). That cut-off and eq(6.19) make the
value of the integral 8(ln|bmax/b90| − [1/2]), where
bmax is the maximum impact parameter, and the
[1/2] term should be dropped since it is an artifact of the
approximation implied by our use of eq(6.59). In the case of
scattering by a plasma, the relevant impact-parameter cut-off is the
length beyond which the collective interactions in the plasma screen
out the electric field of individual nuclei. This distance is called
the Debye length. When the scattering is from neutral atoms, the
relevant cut-off length corresponds to the size of the atom, because
for impact parameters larger than the atom the projectile sees the
whole atom, neutral because of its electrons, rather than a bare
nucleus.
An identical treatment governs the y-component vy, and
consequently the square of the total transverse velocity v⊥2 = vx2+vy2 evolves as
|
|
d〈v⊥2〉
dl
|
= n2 v02(mr/m1)2 πb902 8ln|bmax/b90| , |
| (6.63) |
with bmax approximately the size of the atom.
For small angles θ ≈ v⊥/v and so this equation can
be written in terms of the angle of the scattered velocity direction:
|
|
d〈θ2〉
dl
|
= n2 (mr/m1)2 πb902 8ln|bmax/b90| . |
| (6.64) |
After a finite path length l, there is a distribution of v⊥
with variance
|
〈vx2〉 = 〈vy2〉 = ln2 v02(mr/m1)2 πb902 4ln|bmax/b90| , |
| (6.65) |
which we assume is still small compared to v02 so that small-angle
approximations remain valid.
Because this distribution arises from many independent scatterings, it
becomes Gaussian (following the Central Limit theorem of statistics):
|
f(vx,vy) = | ⎛
⎝
|
1
2π〈vx2〉
| ⎞
⎠
|
exp | ⎧
⎨
⎩
|
− |
(vx2+vy2)
2〈vx2〉
| ⎫
⎬
⎭
|
, |
| (6.66) |
with 〈vx2〉 given by eq(6.65). We may
alternatively regard the Gaussian shape as arising because the
particle distribution is experiencing a diffusion of velocity from
an initial localized distribution (delta function) at v⊥ = 0.
The solution of the diffusion equation in this case is this Gaussian.
The maximum impact parameter (minimum χc) is determined by the
shielding of the nucleus by its atomic electrons. Only for impact
parameters small compared to the atom size, will the projectile see
the bare nucleus because then it penetrates deep inside the electron
shielding cloud. So bmax is approximately the radius of the
electron cloud surrounding the nucleus. This is generally taken to
have a characteristic size approximately10 a0/Z1/3.
There is no mathematical compulsion to cut off the upper limit of the χc
integral short of χc=π, that is s=1. However, if very
energetic particles are involved, the value of b90, which is
inversely proportional to particle energy, becomes very small,
eventually so small that it is smaller than the size of the
nucleus. In that case, the large-angle scattering is affected by the
structure of the nucleus itself and the upper limit is affected. Of
course, this is the basis for experimental high-energy physics
investigations of nuclear structure by electron scattering, but it
requires electron energies greater than roughly Ze2/(4πϵ0rn) ( ≈ Z MeV), where rn is the nuclear radius, of order
10−15 m, and Z its nuclear charge.
6.4 Summary
Collisions of charged particles are governed by the long range Coulomb
force. The range of that force is limited by one of several different
processes, depending on the exact physical situation to a maximum
impact parameter bmax. A minimum impact parameter for the process
is also needed if approximations such as that the collision has a
straight-line trajectory are made, or if quantum effects are
important. Table 6.1 gives a summary of the
situations discussed.
| Impact parameters | Stopping Power (per
electron) |
| Collision Type | bmin | bmax | lnΛ = B/Z |
|
| Classical Coulomb | b90 | γv0/ω | ln[(γv0)/(ωb90)]
|
| Classical energy loss to atoms | | | ln|[(1.123 γ v0)/(〈ω〉b90)]| −[(v02)/(2c2)] |
| Quantum ion loss to atoms | ∼ ħ/γm v | γ v0/ω | ln|[(2γ2 me v02)/(ħ〈ω〉)]| − [(v02)/(c2)] |
| Corrected for inner shell effects | | | ln|[(2γ2 me v02)/(ħ〈ω〉)]| − [(v02)/(c2)] −Ck/Z |
| Quantum electron loss to atoms | ∼ ħ/γm v | γ v0/ω | ln|([(γ+1)/2])1/2 [((γ−1) me c2)/(ħ〈ω〉)]| − [(v02)/(2c2)] |
| Density effect (non-rel. plasma) | b90 | v0/ωp | ln|[(v0)/(ωp b90)]| |
| Angular scattering from nucleus | b90 | ∼ a0/Z1/3 | ln|a0/Z1/3 b90|
|
Table 6.1: Summary of collision calculations.
In collisions of the projectile particle 1,
initial velocity v0, with particles of type 2, density n2, the rate of loss of kinetic energy K per
unit pathlength l is given by
|
|
dK
dl
|
= − K n2 πb902 |
mr2
m1m2
|
8lnΛ = − n2 | ⎛
⎝
|
q1q2
4πϵ0
| ⎞
⎠
|
2
|
|
4π
m2 v02
|
lnΛ |
|
and the angular scattering from nuclei by
|
|
d〈v⊥2〉
dl
|
= v02 n2 πb902 |
mr2
m12
|
8lnΛ = n2 | ⎛
⎝
|
q1q2
4πϵ0
| ⎞
⎠
|
2
|
|
8π
m12 v02
|
lnΛ |
|
with the lnΛ values indicated.
See eqs(6.18) and (6.3) for other definitions.
|