HEAD PREVIOUS

Chapter 5
Atomic Structure and Processes

5.1  Elementary atomic structure

Bohr Orbits correspond to principal quantum number n.
Hydrogen atom energy levels
En = Ry
n2
(5.1)
where the Rydberg energy is
Ry = me
2
 ⎛
⎝ 		e2
4πϵ0ħ
⎞
⎠ 		2

 
 = 13.6 eV   .
(5.2)
The principal quantum number corresponds to the number of nodes of the radial solution of Schrödinger's equation. In the semi-classical treatment of Bohr, the energy of a circular orbit with angular momentum nħ is equal to En, but it is important to realize that in proper quantum mechanics, there are many possible different values of angular momentum for any principal quantum number n (from zero up to approximately nħ.)
The wave function for the hydrogen ground state can be written
ψ = 1
(πa03)1/2
  e−r/a0   ,
(5.3)
where a0 is called the Bohr radius,
a0 = ⎛
⎝ 		ħ
me
⎞
⎠ 		⎛
⎝ 		4πϵ0
e2
⎞
⎠ 		= 5.292×10−11 m   .
(5.4)
Angular momentum of the electron orbit is quantized by a quantum number l. The actual angular momentum is √{l(l+1)} times Planck's constant ħ, which is approximately lħ for large l. The quantum number l can take any integer value up to n−1. For the hydrogen atom the energy levels are (almost) unaffected by l but for multiple-electron atoms the energy differences between different l levels become large. In the wave-function, l is the number of the spherical harmonic (Plm(cosθ)) in its angular variation. Roughly speaking, l is the number of nodes of the wave-function.
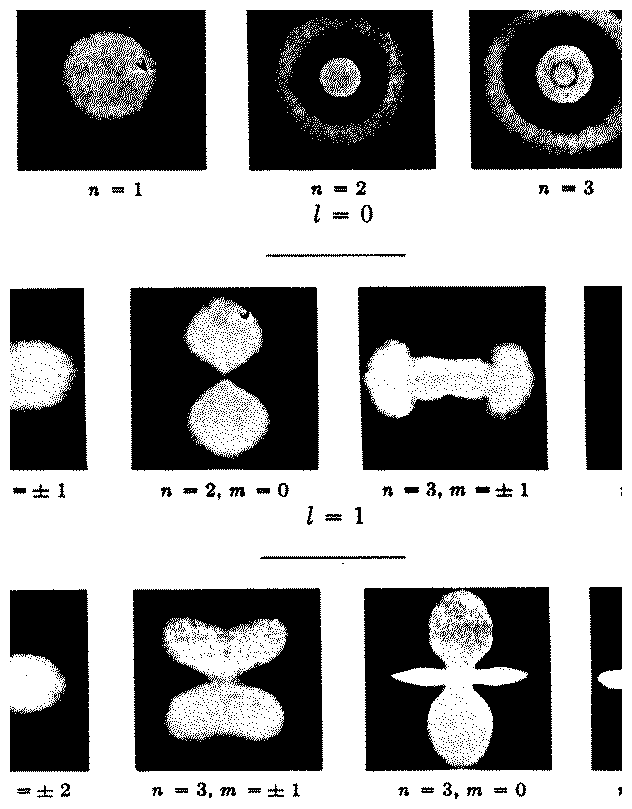
figure/wave_fns.gif
Figure 5.1: Representation of the electron cloud surrounding the nucleus for different quantum numbers. [From Herzberg]
A third quantum number is m which is roughly the component of angular momentum in a certain direction. It can take any value in the sequence −l, −l+1, ..., l−1, l. There are therefore 2l+1 states for each l and n+1 possible l-values, totalling n2 orbital states for each principal quantum level.
Electrons have spin giving rise to (non-orbital) angular momentum ħ/2 and consequently 2 spin states ±1/2. They also satisfy Fermi-Dirac statistics, notably Pauli's exclusion principle, which is that no two electrons can occupy the same quantum state. The two spin states mean that up to two electrons can occupy any orbital state. However, the additional angular momentum of the spin greatly complicates the spectra by shifting the energies, giving rise to doublet states and the whole complexity of atoms.

5.2  Atomic processes in electromagnetic interactions

Atoms can emit or absorb radiation when their electrons make a transition from one quantum state to another. If the energies of the initial and final states are Ei and Ej, then the energy of the photon emitted (or absorbed) is hνij = |Ei − Ej| and obviously the conservation of energy means that Ei must be greater than Ej for emission and less than it for absorption.
Absorption normally takes place by electric dipole transitions. If the energy density of radiation of frequency ν is ρ(ν) per unit frequency (ν), per unit volume, then the transition probability per unit time from the lower to the upper state is written ρ(νij)Bji with the Einstein coefficient, Bji given by Fermi's golden rule
Bji = 8π3
3h2
 Sij
4πϵ0
 = 8π3
3h2
 1
4πϵ0
 ⎢
⎢ 		⌠
⌡ 		ψi erψj*d3r⎢
⎢ 		2
 
    .
(5.5)
The quantity Sij is the square magnitude of the "matrix element" of the atomic dipole moment. (Single quantum states, are considered here to avoid worrying about statistical weight.)
Emission of radiation by the atom if the electron is in the upper state can also be induced by the presence of a radiation field. Its rate per unit time is ρ(νij)Bij with the emission coefficient, Bij equal to the absorption coefficient Bji. Even in the absence of background radiation, "spontaneous" emission occurs with a probability per unit time of Aij = Bij 8πhνij/c3. A typical order of magnitude for 1/Aij, which is the lifetime of the excited state, is nanoseconds. As a result, atoms generally spend most of their time in the ground-state, the state of lowest energy, where electrons fill up all the low energy states as far as possible consistent with the exclusion principle.
Selection rules for which transitions are allowed by electric dipole radiation arise from the fact that the matrix elements, Sij, are zero unless, for example, ∆l = ±1. The energy levels are often illustrated graphically using what is called a "Grotrian" diagram, with energy (often measured in units of cm−1 corresponding to the inverse of the wavelength, 1/λ = E/hc) indicated by height, and angular momentum quantum level on the abscissa. Figure 5.2(a) shows the levels for hydrogen, which has equal energy for different l values. Figure 5.2(b) shows scaled energies for several different elements but with different levels of ionization so that they all possess three electrons, making them "lithium-like". The angular momentum degeneracy is broken, and the active electron can occupy only the principal level n=2 and above, since the n=1 level is already filled with the other two electrons.
(a)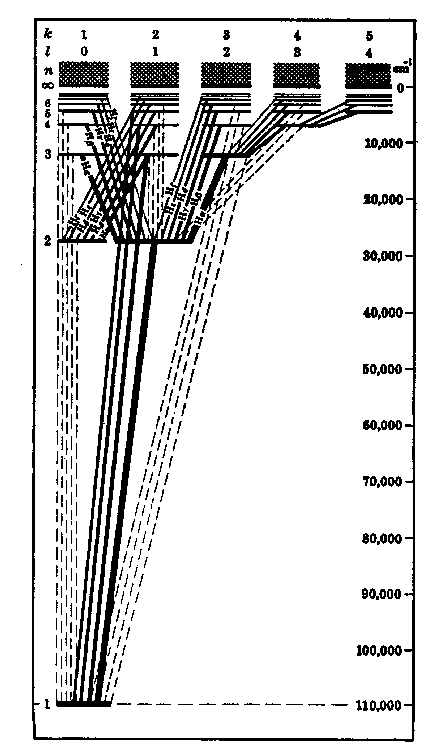figure/grotrian_h.gif       (b)figure/grotrian_Li.gif
Figure 5.2: Energy level diagrams for (a) Hydrogen, indicating the allowed transitions, especially the Balmer series, (b) Lithium-like configurations arising from different stages of ionization, each possessing three electrons.[After Herzberg.]
When both the upper and lower energy states of the electron are bound states, the radiation emission occurs as a discrete narrow line at the specific frequency νij. Line radiation is characteristic of a particular element and is one of the most powerful means of identification. However, transitions can also occur between bound states and free electron states. In the case of a downward transition, this is a process of "recombination" whereby an initially ionized atom recombines with a free electron, emitting the excess energy in the form of an electromagnetic photon, and forming a composite atom. In that case, because there is a continuous range of possible kinetic energies for the free electron (unlike the situation with a bound upper state) there is a continuous spectrum of electromagnetic radiation from this process. The opposite process is when a photon excites an initially bound electron into a free state. This is the process of photo-ionization of an atom, known more colloquially as the photoelectric effect.
For multiple-electron atoms the electrons are said to reside in "shells". These shells correspond to the principal quantum levels. The lowest energy states, corresponding to electrons bound most strongly to the nucleus, are the n=1 level, known as the K-shell. The next n=2 level is known as the L-shell, and so on. An atom of a relatively heavy element has several shells filled with electrons. For example copper has the K, L, and M-shells filled and one electron in the N-shell. The easiest electron to remove from the atom is the electron in the highest energy state. Its binding energy determines the "ionization energy" of the element, that is, the energy that needs to be provided to strip the electron off (7.72 eV for copper). The K-shell electrons are much more strongly bound. Their binding energy is roughly Z2Ry, (more precisely, for copper 9.0 keV, corresponding to a wavelength of 0.138 nm).
If a photoelectric absorption removes an inner shell (e.g. K-shell) electron, as is often the case, then the resulting partially ionized atom is left in an excited state. Moreover, the excitation energy far exceeds the ionization energy of the resulting atom. There is, then, a hole in a very deep shell and electrons from other higher shells can liberate a lot of energy (roughly the K-shell binding energy) if they make a transition down into the hole. One of the easiest ways for this transition to occur is for the excess energy to be given to one of the weakly bound electrons in the highest shell. Since the energy exceeds the ionization energy, the weakly bound electron becomes completely unbound and is ejected from the atom with the excess energy less its binding energy appearing in its kinetic energy. This process is called the Auger effect (or sometimes "autoionization") and the ejected electrons are called Auger electrons.

5.3  The Photoelectric Effect

It is interesting to contrast the photoelectric effect with Compton scattering. Both of these processes describe a photon interacting with an electron, transferring energy to it, and ejecting it from its atom. The key differences are
The cross-section for photoelectric absorption is not straightforward to calculate rigorously. Some of the earliest calculations, prior to the full development of quantum mechanics (Kramers 1923), used classical radiation theory and the "correspondence principle" to obtain (quite accurate) estimates based on a calculation of the inverse process, radiative recombination, and hence deducing the photoelectric cross-section from equilibrium arguments and the principle of detailed balance. These non-relativistic calculations can be carried through using the bremsstrahlung formulism we shall discuss later, but the time is probably not well spent here. The result of these calculations is to obtain a cross-section for absorption by a single K-shell electron of photons with energy above the K-shell binding energy in the form
σp = ⎡
⎣ 		G 32π2
3√3
  re2⎤
⎦ 		α3 Z4⎛
⎝ 		mec2
hν
⎞
⎠ 		3

 
    .
(5.6)
where α is the fine structure constant ( ≈ 1/137), Z is the nuclear charge, hν = E is the photon energy, and G is a numerical factor of order unity. Notice that the square bracket factor is roughly seven times the Thomson cross-section (8πre2/3).
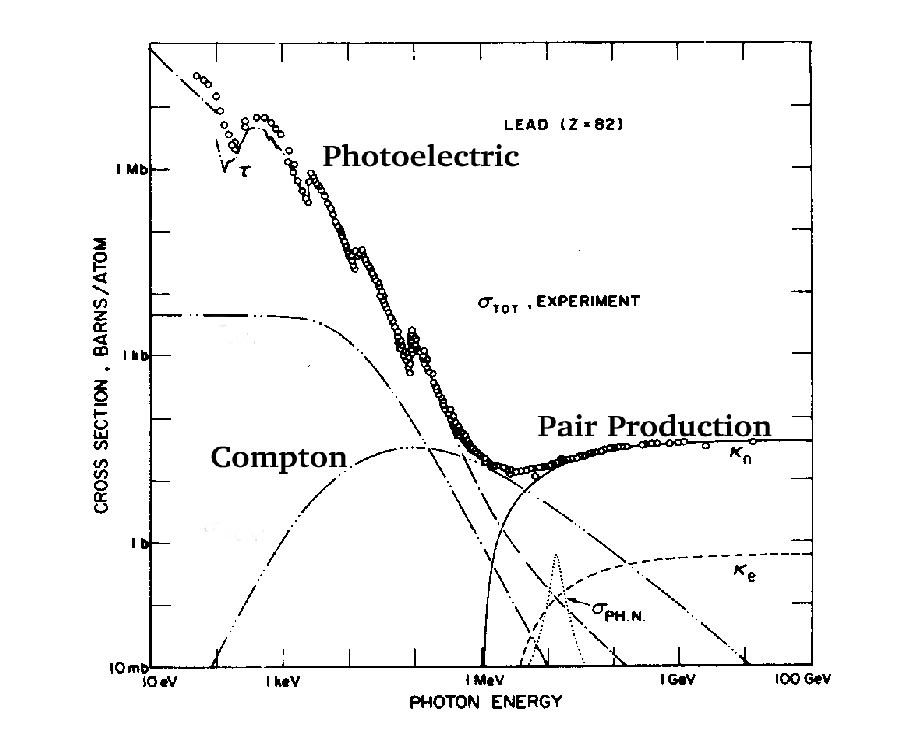
figure/photon_processes.gif
Figure 5.3: Photon absorption processes for Lead. At low energy the photoelectric effect dominates, and the absorption edges for the different shells are visible. [From H.Anderson, Ed.]
The most important feature, however, is the rapid increase of the cross-section ( ∝ E−3) as the photon energy decreases. This cross-section applies only down to a photon energy equal to the K-shell binding energy. There is therefore an "absorption edge" in the cross-section at that energy. Below that, the photon has insufficient energy for photoionization to occur for K-shell electrons and the absorption drops abruptly. However, L-shell electrons can be ejected down to an energy about 1/n2=1/4 of the K-shell energy, so they remain active, and N-shell electrons to even lower energies than that and so on, giving rise to an absorption edge for each shell. The higher shells have intrinsically lower cross-section (by classically 1/n3 per electron) but because of the strong E−3 energy dependence, the total cross-section still maintains an upward trend at decreasing photon energy, as illustrated in Figure 5.3.
At higher energies, where relativistic effects are important for the ejected electrons, the dependence on photon energy becomes weaker. The reason for this is predominantly the fact that the electron's velocity becomes constant (equal to c) and, in the limit E >> mec2, its momentum, which determines its quantum phase-space, becomes proportional to energy (rather than square-root of energy non-relativistically). The effect is to reduce the power of the photon energy dependence to σ ∝ E−1.
A different, often cited, approximation for the non-relativistic photoelectric cross-section accounting for both K-shell electrons is [H.Hall, Rev. Mod. Phys. 8, 358 (1936)]
σp = 4√2 Z5 α4 ⎛
⎝ 		mec2
hν
⎞
⎠ 		3.5

 
 σThomson   .
(5.7)
while for the strongly relativistic case, E >> mec2 the formula
σp = 1.5 Z5 α4 ⎛
⎝ 		mec2
hν
⎞
⎠ 		σThomson
(5.8)
may be used. [Each of these expressions is the cross-section per atom].
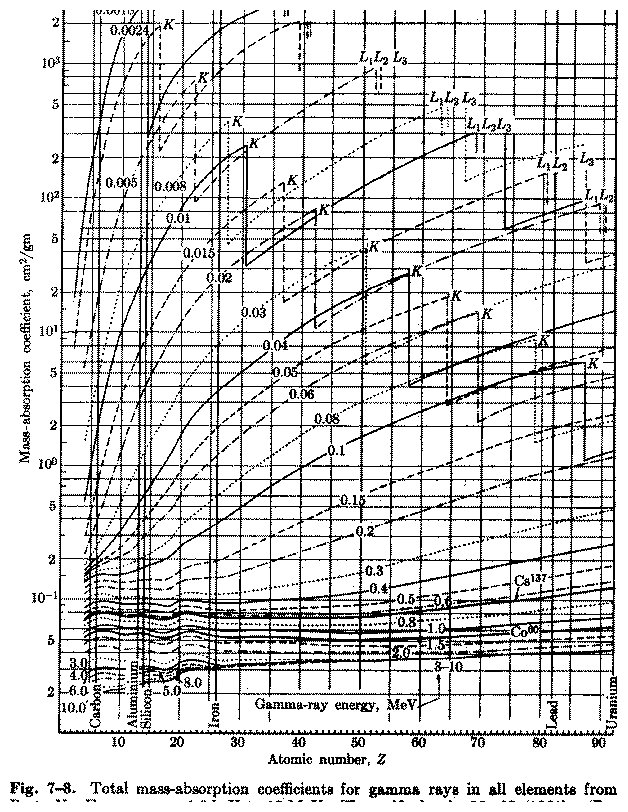
A comprehensive graphical representation for total photon absorption down to 1.8 keV energy is given in Figure 5.4
figure/mass_absorption.gif
Figure 5.4: Absorption coefficients for all elements. [From Enge]

5.4  Electrons and Pair Production

In 1928 Paul Dirac, by a master-stroke of mathematical insight, developed a theory of the electron that combines quantum mechanics consistently with relativity. The theory predicted many hitherto unsuspected phenomena including especially electron spin, but also that there exist electron states of negative energy. In order to explain why electrons do not immediately make a transition from their positive energy state to a negative energy state, Dirac postulated that all the negative states are full. In that case, a vacancy or "hole" in the negative energy states, which naturally has positive energy with respect to a fully-occupied situation, behaves just like an electron except that its charge is positive. Thus the positron was predicted. Actually, Dirac first thought that the holes might correspond to protons. 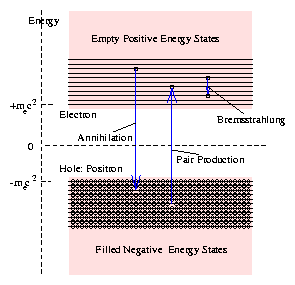However a few years later, when the first experimental evidence of positrons was observed, he immediately saw this as confirmation of his theory.
When a positron - a hole in the otherwise full negative energy states - and an electron encounter one another, a downward transition of the electron into the lower, negative energy, state can occur. The electron fills up the hole, annihilating both particles; its energy becomes negative; and the rest energy (2mec2) and kinetic energy of the two particles appears as a photon. The analogy with a electron transition in an atom is helpful, although this situation really involves two free states of the electron, so it is more closely allied to bremsstrahlung.
figure/pair_schematic.gif
Figure 5.5: Schematic diagram of positive and negative energy electron states, annihilation and pair production.
Like any elementary quantum process, electron-positron annihilation has an inverse process: pair production. Pair production occurs when a photon with energy exceeding 2mec2 produces an electron and a positron, absorbing all the photon's energy, through interaction with a neighboring charge (usually a nucleus). The presence of the neighboring charge is necessary as a perturbation to couple the photon to the electron field and to absorb some of the photon's momentum, which cannot be completely transfered to the electron/positron pair because their ratio of momentum to energy is always lower than that of a photon (1/c).
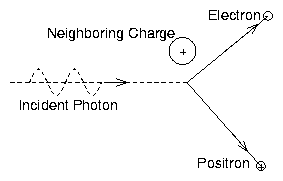
figure/pair_production.gif
Figure 5.6: Pair production by an energetic photon in the presence of a neighboring charge.
We are not in a position without extensive relativistic quantum mechanics to calculate the cross-section. Its value proves to be a weak (logarithmic) function of the photon energy in the range 2mec2 << hν << mec2 Z−1/3 α−1
σpp ≈ Z2 α re2 ⎛
⎝ 		28
9
 ln 2hν
mec2
 − 218
27
⎞
⎠ 		   .
(5.9)
Qualitatively, one can understand these factors as follows. The Z2 factor arises from the strength of the perturbative coupling by a nucleus of atomic charge Z. The fine structure constant α ≡ e2/4πϵ0ħ c and the classical electron radius re ≡ e2/4πϵ0mec2 are characteristic of coupling between electromagnetic photons and the electron. The cross-section becomes essentially constant for very high photon energy hν >> mec2 Z−1/3 α−1 because of shielding of the nucleus by its bound electrons. Naturally the cross-section falls to zero as the photon energy is lowered towards 2mec2 = 1.02 MeV. These characteristics are illustrated in Figure 5.3. That figure also shows the coefficient for pair production in interaction with electrons. It is negligible for heavy elements since the nucleus is slightly more than Z2 times as effective as an electron and there are only Z electrons per nucleus. So the total attenuation due to all electrons is approximately 1/Z times that of the nuclei.
Table 5.1: Atomic Parameters: Definitions and Values


Rydberg Energy Ry (me/2)(e2 / 4πϵ0ħ)2 13.61 eV
Bohr Radius a0 ħ2 4πϵ0/e2 me 5.292×10−11 m
Fine Structure Constant α e2/4πϵ0ħ c 1/137.04
Classical Electron Radius re e2/4πϵ0 me c22.818×10−15 m
Thomson Cross-Section σT 8πre2/3 6.652×10−29 m
Relationships α2 = 2 Ry/me c2
2Ry a0 = e2/4πϵ0 = αħ c
re = a0 α2
ħ = me c a0 α = me c re /α
HEAD NEXT