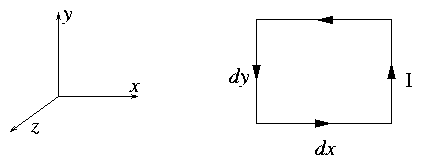Chapter 2
Particle Motion in Electric and Magnetic Fields

Considering E and B to be given, we study the trajectory of particles under the influence of Lorentz force

F = q ( E+ v∧B)

(2.1)

2.1 Electric Field Alone

= q E

(2.2)

Orbit depends only on ratio q/m. Uniform E ⇒ uniform acceleration. In one-dimension z, E_z trivial. In multiple dimensions directly analogous to particle moving under influence of gravity. Acceleration gravity g ↔ ^q/_m E. Orbits are parabolas.

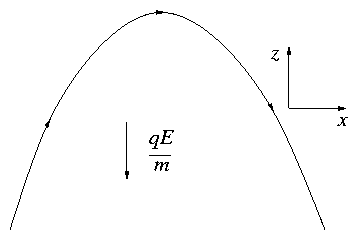
Figure 2.1: In a uniform electric field, orbits are parabolic, analogous to gravity.

Energy is conserved taking into account potential energy

P.E. = q ϕ electric potential

(2.3)

[Proof if needed, regardless of E spatial variation,

. v

−q ∇ϕ. v= −q

dϕ

(2.4)

⎛
⎝

m v²

⎞
⎠

−

( q ϕ)

(2.5)

i.e. ¹/₂ mv² + q ϕ = const.]

A particle gains kinetic energy qϕ when falling through a potential drop −ϕ. So consider the acceleration and subsequent analysis of particles electrostatically:

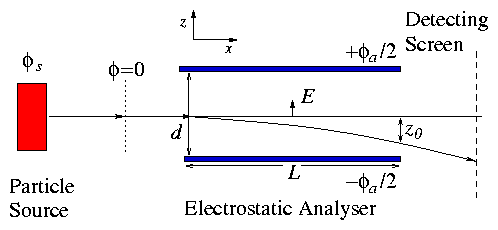
Figure 2.2: Schematic of electrostatic acceleration and analysis.

How much deflection will there be? After acceleration stage KE = ¹/₂ m v_x² = qϕ_s

v_x =

⎛
√

2qϕ_s

(2.6)

Supposing E_a, field of analyser, to be purely ∧z, this velocity is subsequently constant. Within the analyser

dv_z

= q E_a⇒ v_z =

E_a t =

E_a

v_x

(2.7)

z =

⌠
⌡

v_z dt =

E_a

t²

E_a

x²

v_x²

(2.8)

Hence height at output of analyser is

z_o

E_a

L²

v_x²

E_a

L²

2qϕ_s

−

E_a

ϕ_s

L² = +

ϕ_a

ϕ_s

L²

(2.9)

using E_a = −ϕ_a / d. Notice this is independent of q and m! We could see this directly by eliminating the time from our fundamental equations noting

= v

( = v. ∇) with v =

⎛
√

2q ( ϕ− ϕ_s )

or v =

⎛
√

⎛
⎝

ϕ− ϕ_s +

E_s

⎞
⎠

(2.10)

if there is initial energy E_s. So equation of motion is

⎛
√

2q ( ϕ_s − ϕ)

⎛
⎜
⎝

⎛
√

2q( ϕ_s − ϕ)

⎞
⎟
⎠

= 2

√

ϕ_s − ϕ

√

ϕ_s − ϕ

=E_a = − ∇ϕ ,

(2.11)

which is independent of q and m. Trajectory of particle in purely electrostatic field depends only on the field (and initial particle kinetic energy/q). If initial energy is zero, can't deduce anything about q,m.

2.2 Electrostatic Acceleration and Focussing

Accelerated charged particle beams are widely used in science and in everyday applications.

Examples:

X-ray generation from e-beams (Medical, Industrial)
Electron microscopes
Welding. (e-beam)
Surface ion implantation
Nuclear activation (ion-beams)
Neutron generation
Television and (CRT) Monitors (fading!)

For applications requiring <~ few hundred keV energy electrostatic acceleration is easiest, widest used. Schematically

Figure 2.3: Obtaining defined energy from electrostatic acceleration is straightforward in principle. Beam focussing and transport to the target is crucial.

Clearly getting the required energy is simple. Ensure the potential difference is right and particles are singly charged: Energy (eV) ↔ Potential V. More interesting question: How to focus the beam? What do we mean by focussing?

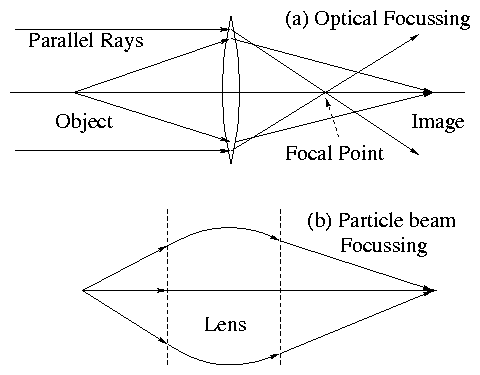
Figure 2.4: Analogy between optical and particle-beam focussing.

What is required of the "Lens"? To focus at a single spot we require the ray (particle path) deviation from a "thin" lens to be systematic. Specifically, all initially parallel rays converge to a point if the lens deviates their direction by θ such that

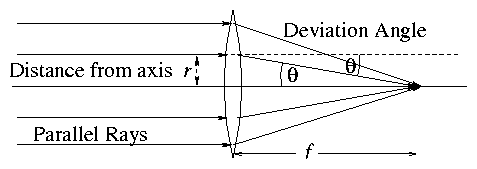
Figure 2.5: Requirement for focussing is that the angular deviation of the path should be a linear function of the distance from the axis.

r = f tanθ

(2.12)

and for small angles, θ, r = f θ. This linear dependence (θ = r/f)) of the deviation θ, on distance from the axis, r, is the key property. Electrostatic Lens would like to have (e.g.)

E_r =

E_a

(2.13)

but the lens can't have charged solids in its middle because the beams must pass through so (initially) ρ = 0 ⇒ ∇. E = 0. Consequently pure E_r is impossible (0 = ∇. E = ¹/_r ∂(r E_r)/ ∂r = 2E_a /a ⇒ E_a = 0). For an axisymmetric lens (∂/∂θ = 0) we must have both E_r and E_z.

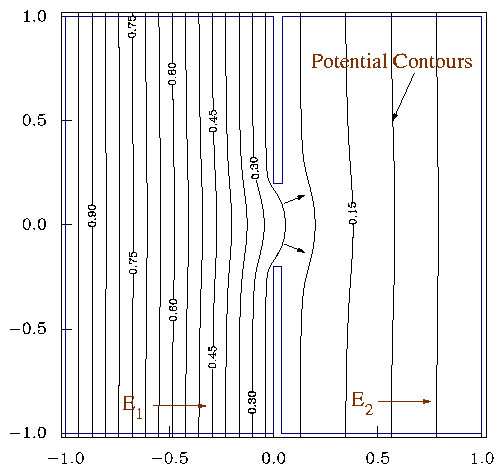
Figure 2.6: Potential variation near an aperture between two regions of different electric field gives rise to focussing.

Perhaps the simplest way to arrange appropriate E_r is to have an aperture between two regions of unequal electric field. The potential contours "bow out" toward the lower field region: giving E_r.

Calculating focal length of aperture Radial acceleration.

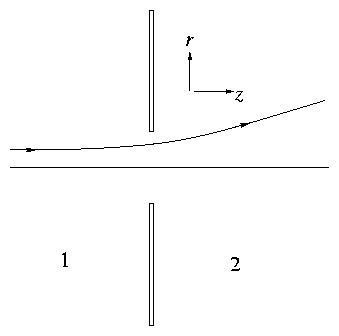
Figure 2.7: Coordinates near an aperture.

dv_r

E_r

(2.14)

dv_r

v_z

dv_r

E_r

v_z

(2.15)

But

∇. E= 0 ⇒

∂( r E_r )

∂r

∂E_z

∂z

= 0

(2.16)

Near the axis, only the linear part of E_r is important i.e.

E_r (r, z) ≅ r

∂E_r

∂r

⎢
⎢

r=0

(2.17)

∂

∂r

r E_r ≅ 2

∂E_r

∂r

⎢
⎢

r=0

(2.18)

and thus

∂E_r

∂r

⎢
⎢

r=0

∂E_z

∂z

= 0

(2.19)

and we may write E_r ≅ − ¹/₂ r ∂E_z/∂z. Then

dv_r

= −

q r

2mv_z

∂E_z

∂z

(2.20)

which can be integrated approximately assuming that variations in r and v_z can be neglected in lens to get

δv_r = [ v_r ]^final_initial =

− q r

2mv_z

[E_z ]²₁

(2.21)

The angular deviation is therefore

θ =

− δv_r

v_z

+q r

2mv_z²

[E_z2 − E_z1 ]

(2.22)

and the focal length is f = r/θ

f =

2mv_z²

q( E_z2 − E_z1 )

4 E

q ( E_z2 − E_z1 )

(2.23)

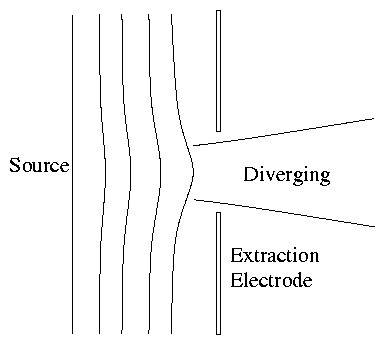
When E₁ is an accelerating region and E₂ is zero or small the lens is diverging. This means that just depending on an extractor electrode to form an ion beam will give a diverging beam.

Figure 2.8: The extraction electrode alone always gives a diverging beam.

Need to do more focussing down stream: more electrodes.

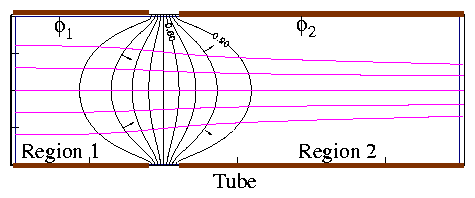
2.2.1 Immersion Lens

Two tubes at different potential separated by gap

Figure 2.9: An Immersion Lens consists of adjacent sections of tube at different potentials.

In this case the gap region can be thought of as an aperture but with the electric fields E₁, E₂ the same (zero) on both sides. Previous effect is zero. However two other effects, neglected previously, give focussing:

v_z is not constant.
r is not constant.

Consider an accelerating gap: q(ϕ₂ − ϕ₁) < 0.

Effect (1) ions are converged in region 1, diverged in region 2. However because of z-acceleration, v_z is higher in region 2. The diverging action lasts a shorter time. Hence overall converging.

Effect (2) The electric field E_r is weaker at smaller r. Because of deviation, r is smaller in diverging region. Hence overall converging.

For a decelerating gap you can easily convince yourself that both effects are still converging. [Time reversal symmetry requires this.] One can estimate the focal length as

≅

q²

E²

⌠
⌡

⎛
⎝

∂ϕ

∂z

⎞
⎠

⎢
⎢

r=0

dz (for weak focussing)

(2.24)

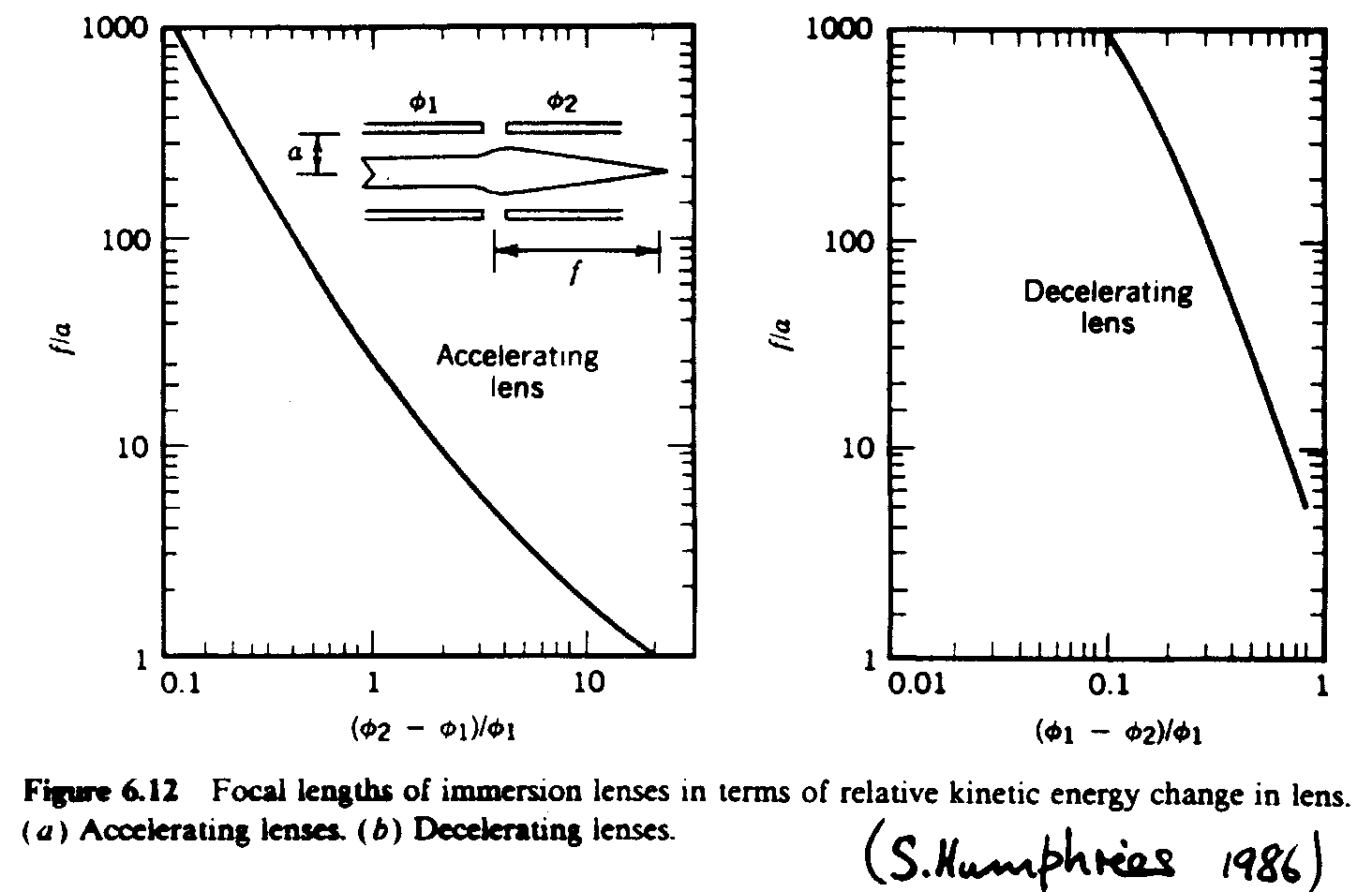
but numerical calculations give the values in figure 2.10 where ϕ₁ = E/q. Here E is the energy in region 1.

Figure 2.10: Focal length of Electrostatic Immersion Lenses. Dependence on energy per unit charge (ϕ) in the two regions, from S.Humphries 1986

Effect (2) above, that the focussing or defocussing deviation is weaker at points closer to the axis, means that it is a general principle that alternating lenses of equal converging and diverging power give a net converging effect. This principle can be considered to be the basis for

2.2.2 Alternating Gradient Focussing

Idea is to abandon the cylindrically symmetric geometry so as to obtain stronger focussing. Consider an electrostatic configuration with E_z = 0 and

E_x =

dE_x

x with

dE_x

= const.

(2.25)

Since ∇. E = 0, we must have

dE_x

dE_y

= 0 ⇒

dE_y

= const ⇒ E_y = −

dE_x

(2.26)

This situation arises from a potential

ϕ = ( x² − y² )

⎛
⎝

dE_x

⎞
⎠

(2.27)

so equipotentials are hyperbolas x² − y² = const. If qdE_x/dx is negative, then this field is converging in the x-direction, but dE_y/dy = − dE_x/dx, so it is, at the same time, diverging in the y-direction. By using alternating sections of +ve and -ve dE_x/ dx a net converging focus can be obtained in both the x and y directions. This alternating gradient approach is very important for high energy particle accelerators, but generally magnetic, not electrostatic, fields are used. So we'll go into it more later.

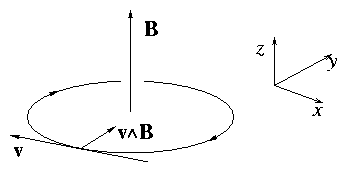
2.3 Uniform Magnetic field

= q ( v∧B)

(2.28)

Take B in ∧z-direction. Never any force in ∧z-dir. ⇒ v_z = constant. Perpendicular dynamics are separate.

Figure 2.11: Orbit of a particle in a uniform magnetic field.

2.3.1 Brute force solution:

⋅

v_y B

⋅

−q

v_x B

(2.29)

⇒

⋅⋅

−

⎛
⎝

⎞
⎠

v_x

⋅⋅

= −

⎛
⎝

⎞
⎠

v_y

(2.30)

Solution

v_x = v sin

v_y = v cos

x = −v

cos

t + x₀

y = v

sin

t + y₀

(2.31)

the equation of a circle. Center (x₀, y₀) and radius ( v m/qB ) are determined by initial conditions.

2.3.2 `Physics' Solution

Magnetic field force does no work on particle because F ⊥v. Consequently total |v| is constant.
Force is thus constant, ⊥ to v. Gives rise to a circular orbit.
Centripetal acceleration gives [(v²)/r] = [Force/mass] = q [vB/m] i.e. r = [mv/qB]. This radius is called the Larmor (or gyro) Radius.
Frequency of rotation ^v/_r = [qB/m] ≡ Ω is called the "Cyclotron" frequency (angular frequency, s⁻¹, not cycles/sec, Hz).

When we add the constant v_z we get a helical orbit. Cyclotron frequency Ω = qB/m depends only on particle character q,m and B-strength not v (non relativistically, see aside). Larmor Radius r = mv/qB depends on particle momentum mv. All (non-relativistic) particles with same q/m have same Ω. Different energy particles have different r. This variation can be used to make momentum spectrometers.

2.3.3 Relativistic Aside

Relativistic dynamics can be written

p = q ( [ E+ ] v∧B)

(2.32)

where relativistic momentum is

p = m v=

m₀ v

⎛
√

1 −

v²

c²

(2.33)

Mass m is increased by factor

γ =

⎛
⎝

1 −

v²

c²

⎞
⎠

−¹/₂

(2.34)

relative to rest mass m₀. Since for E = 0 the velocity |v| = const, γ is also constant, and so is m. Therefore dynamics of a particle in a purely magnetic field can be calculated as if it were non-relativistic: m dv/dt = q (v∧B), except that the particle has mass greater by factor γ than its rest mass.

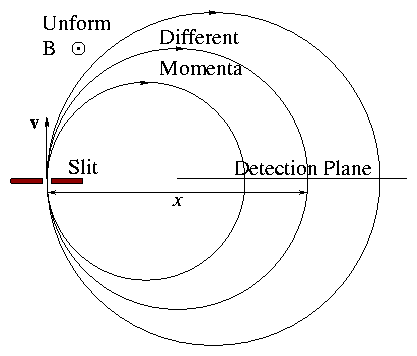
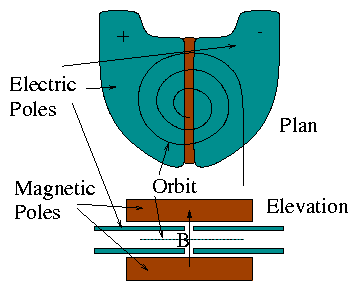
2.3.4 Momentum Spectrometers

Particles passing vertically through slit take different paths depending on mv/q.

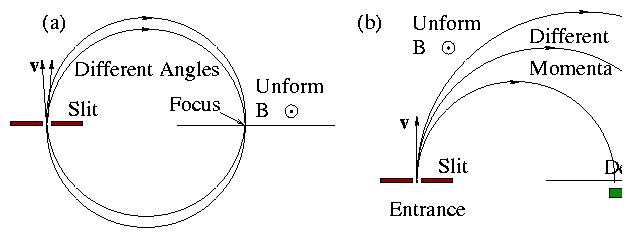
Figure 2.12: Different momentum particles strike the detection plane at different positions.

By measuring where a particle hits the detection plane we measure its momentum/q :

= x :

(2.35)

Why make the detection plane a diameter? Because detection position is least sensitive to velocity direction. This is a form of magnetic focussing. Of course we don't need to make the full 360^°, so analyser can be reduced in size.

Figure 2.13: (a) Focussing is obtained for different input angles by using 180 degrees of orbit. (b) The other half of the orbit is redundant.

Even so, it may be inconvenient to produce uniform B of sufficient intensity over sufficiently large area if particle momentum is large.

2.3.5 Historical Day Dream (J.J. Thomson 1897)

"Cathode rays": how to tell their charge and mass?

Electrostatic Deflection

Tells only their energy/q = E/q and we have no independent way to measure E since the same quantity E/q just equals accelerating potential, which is the thing we measure.

Magnetic Deflection

The radius of curvature is

r =

(2.36)

So combination of electrostatic and electromagnetic gives us

mv²

= M₁ and

= M₂

(2.37)

Hence

2M₁

M₂²

(2.38)

We can measure the charge/mass ratio. In order to complete the job an independent measure of q (or m) was needed. Millikan (1911-13). [Actually Townsend in J.J. Thomson's lab had an experiment to measure q which was within ∼ factor 2 correct.]

2.3.6 Practical Spectrometer

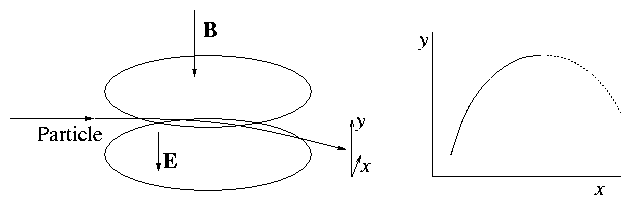
In fusion research fast ion spectrum is often obtained by simultaneous electrostatic and electromagnetic analysis E parallel to B. This allows determination of E/q and q/m ⇒ velocity of particle [E = ¹/₂ m v²].

Figure 2.14: E parallel to B analyser produces parabolic output locus as a function of input velocity. The loci are different for different q/m.

Thus e.g. deuterons and protons can be distinguished. However, He⁴ and D² have the same ^q/_m so one can't distinguish their spectra on the basis of ion orbits.

2.4 Dynamic Accelerators

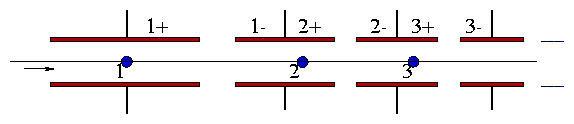
In addition to the electrostatic accelerators, there are several different types of accelerators based on time-varying fields. With the exception of the Betatron, these are all based on the general principle of arranging for a resonance between the particle and the oscillating fields such that energy is continually given to the particle. Simple example

Figure 2.15: Sequence of dynamically varying electrode potentials produces continuous acceleration. Values at 3 times are indicated.

Particle is accelerated through sequence of electrodes 3 at times (1) (2) (3). The potential of electrode is raised from negative to +ve while particle is inside electrode. So at each gap it sees an accelerating E_z. Can be thought of as a successive moving potential hill:

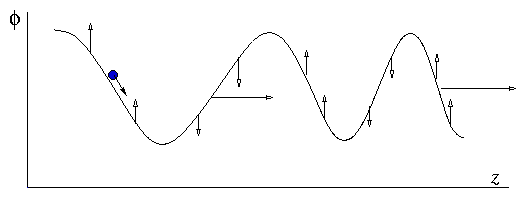
Figure 2.16: Oscillating potentials give rise to a propagating wave.

"Wave" of potential propagates at same speed as particle so it is continuously accelerated. Historically earliest widespread accelerator based on this principle was the cyclotron.

2.4.1 Cyclotron

Figure 2.17: Schematic of a Cyclotron accelerator.

Take advantage of the orbit frequency in a uniform B-field Ω = [qB/m]. Apply oscillating potential to electric poles, at this frequency. Each time particle crosses the gap (twice/turn) it sees an accelerating electric field. Resonant frequency

f =

Ω

2π

m2π

= 1.52 ×10⁷B Hz

(2.39)

15.2 MHz/T for protons. If magnet radius is R particle leaves accelerator when its Larmor radius is equal to R

= R ⇒

mv² =

q²

B² R²

(2.40)

If iron is used for magnetic pole pieces then B <~2T (where it saturates). Hence larger accelerator is required for higher energy E ∝ R². [But stored energy in magnet ∝ R² → R³].

2.4.2 Limitations of Cyclotron Acceleration: Relativity

Mass increase ∝ (1 − v²/c²)^−¹/₂ breaks resonance, restricting maximum energy to ∼ 25MeV (protons). Improvement: sweep oscillator frequency (downward). "Synchrocyclotron" allowed energy up to ∼ 500MeV but reduced flux. Alternatively: Increase B with radius. Leads to orbit divergence parallel to B. Compensate with azimuthally varying field for focussing AVF-cyclotron. Advantage continuous beam.

2.4.3 Synchrotron

Vary both frequency and field in time to keep beam in resonance at constant radius. High energy physics (to 800 GeV).

2.4.4 Linear Accelerators

Avoid limitations of electron synchrotron radiation. Come in 2 main types. (1) Induction (2) RF (linacs) with different pros and cons. (RF for highest energy electrons). Electron acceleration: v=c different problems from ion.

2.5 Magnetic Quadrupole Focussing (Alternating Gradient)

Magnetic focussing is preferred at high particle energy. Why? Its force is stronger.
Magnetic force on a relativistic particle qcB.
Electric force on a relativistic particle qE.
E.g. B=2T ⇒ cB = 6 ×10⁸ same force as an electric field of magnitude 6 ×10⁸ V/m = 0.6MV/mm! However magnetic force is perpendicular to B so an axisymmetric lens would like to have purely azimuthal B field

Figure 2.18: Impossible ideal for magnetic focussing: purely azimuthal magnetic field.

B= ∧θ B_θ. However this would require a current right where the beam is:

⌠
(⎜)
⌡

B. dl = μ_o I .

(2.41)

Axisymmetric magnetic lens is impossible. However we can focus in one cartesian direction (x,y) at a time. Then use the fact that successive combined focus-defocus has a net focus.

2.5.1 Preliminary Mathematics

Consider [(∂)/(∂z)] = 0 purely transverse field (approx) B_x, B_y. This can be represented by B = ∇∧A with A = ∧z A so ∇∧A = ∇∧(∧z A) = − ∧z ∧∇A (since ∇∧z = 0). In the vacuum region j = 0 (no current) so

0 = ∇∧B= ∇∧

⎛
⎝

−

∧∇A

⎞
⎠

= −

∇² A +

⎛
⎝

. ∇

⎞
⎠

∇A

(2.42)

i.e. ∇²A = 0. A satisfies Laplace's equation. Notice then that solutions of electrostatic problems, ∇² ϕ = 0 are also solutions of (2-d) vacuum magnetostatic problems. The same solution techniques work.

2.5.2 Multipole Expansion

Potential can be expanded about some point in space in a kind of Taylor expansion. Choose origin at point of expansion and use coordinates (r,θ), x = r cosθ, y = r sinθ.

∇² A =

∂

∂r

∂A

∂r

r²

∂² A

∂θ²

= 0

(2.43)

Look for solutions in the form A = u(r) . w(θ). These require

d²w

dθ²

= − const. ×w

(2.44)

and

= const. ×u.

(2.45)

Hence w solutions are sines and cosines

w = cosn θ or sinn θ

(2.46)

where n² is the constant in the previous equation and n integral to satisfy periodicity. Correspondingly

u = rⁿ or lnr , r⁻ⁿ

(2.47)

These solutions are called "cylindrical harmonics" or (cylindrical) multipoles:

lnr

rⁿ cosn θ

r⁻ⁿ cosnθ

rⁿ sinn θ

r⁻ⁿ sinn θ

(2.48)

If our point of expansion has no source at it (no current) then the right-hand column is ruled out because no singularity at r=0 is permitted. The remaining multipoles are

1	constant irrelevant to a potential
r cosθ(=x)	uniform field, ∇A ∝ ∧x
r² cos2 θ = r² (cos² θ− sin² θ) = x²−y²	non-uniform field
Higher orders	neglected.

The second order solution, x²−y² is called a "quadrupole" field (although this is something of a misnomer). [Similarly r³ cos3 θ→ "hexapole", r⁴ cosθ "octupole".] We already dealt with this potential in the electric case.

∇A = ∇( x² − y² ) = 2 x

− 2y

(2.49)

−

∧∇A = − 2x

−2y

(2.50)

Force on longitudinally moving charge:

q v∧B= q v∧( ∇∧A)

(2.51)

− q v∧

⎛
⎝

∧∇A

⎞
⎠

= q

⎛
⎝

⎞
⎠

∇A ≡ q v_z ∇A

(2.52)

Magnetic quadrupole force is identical to electric `quadrupole' force replacing

ϕ↔ −Av_z

(2.53)

Consequently convergence in x-direction ⇒ divergence in y-direction but alternating gradients give net convergence. This is basis of all "strong focussing".

2.6 Force on distributed current density

We have regarded the Lorentz force law

F = q ( E+ v∧B)

(2.54)

as fundamental. However forces are generally measured in engineering systems via the interaction of wires or conducting bars with B-fields. Historically, of course, electricity and magnetism were based on these measurements. A current (I) is a flow of charge: Coulombs/s ≡ Amp. A current density j is a flow of charge per unit area A/m². The charge is carried by particles:

j =

∑
species i

n_i v_i q_i

(2.55)

Hence total force on current carriers per unit volume is

F =

∑
i

n_i q_i ( v_i ∧B) = j ∧B

(2.56)

Also, for a fine wire carrying current I, if its area is Ω, the current density averaged across the section is

j =

Ω

(2.57)

Volume per unit length is Ω. And the force/unit length = Ωj ∧B = I ×B perpendicular to the wire.

2.6.1 Forces on dipoles

We saw that the field of a localized current distribution, far from the currents, could be approximated as a dipole. Similarly the forces on a localized current by an external magnetic field that varies slowly in the region of current can be expressed in terms of magnetic dipole. [Same is true in electrostatics with an electric dipole].

Total force

F =

⌠
⌡

j ∧Bd³x′

(2.58)

where B is an external field that is slowly varying and so can be approximated as

B( x′) = B₀ + ( x′. ∇) B

(2.59)

where the tensor ∇B( ∂B_j/∂x_i) is simply a constant (matrix). Hence

⌠
⌡

j ∧B_o + j ∧( x′. ∇B) d³x′

⎛
⎝

⌠
⌡

j d³x′

⎞
⎠

∧B_o +

⌠
⌡

j ∧( x′. ∇B) d³x′

(2.60)

The first term integral is zero and the second is transformed by our previous identity, which can be written for any vector x as

x∧

⌠
⌡

( x′∧j ) d³x′ = 2 x.

⌠
⌡

j x′d³x′ = − 2 x.

⌠
⌡

x′j d³x′

(2.61)

Use the quantity ∇B (constant evaluated at origin) for x (i.e. x_i ↔[(∂)/(∂x_i)] B_j) giving

⌠
⌡

( x′∧j ) d³x ∧∇B= m ∧∇B=

⌠
⌡

j ( x′. ∇) Bd³x

(2.62)

This tensor identity is then contracted by an `internal' cross-product [ϵ_ijkT_jk] to give the vector identity

( m ∧∇) ∧B=

⌠
⌡

j ∧[ ( x′. ∇) B]d³x

(2.63)

If this internal cross product seems confusing, think of it this way. Our identity (2.61) is for any x. Choose to write it for x ↔ ∇:

m∧∇ =

⌠
⌡

j x′d³x′.∇ .

(2.64)

Now cross multiply both sides of this equation with B on the right:

(m∧∇)∧B =

⌠
⌡

j x′d³x′ .∇∧B =

⌠
⌡

j ∧[ ( x′ . ∇) B] d³x = F

(2.65)

Either way we get

F = ( m ∧∇) ∧B=∇( m . B) − m ( ∇. B)

(2.66)

(remember the ∇ operates only on B not m). This is the force on a dipole:

F = ∇( m . B) .

(2.67)

Total Torque (Moment of force)

⌠
⌡

x′∧( j ∧B)d³ x′

(2.68)

⌠
⌡

j ( x′. B) − B( x′. j ) d³x′

(2.69)

B here is (to lowest order) independent of x′: B₀ so second term is zero since

⌠
⌡

x′. j d³x′ =

⌠
⌡

{ ∇′.( |x′|² j ) − |x′|² ∇′. j }d³ x′ = 0.

(2.70)

The first term is of the standard form of our identity.

M = B.

⌠
⌡

x′j d³ x′ = −

B∧

⌠
⌡

( x′∧j ) d³x′

(2.71)

M = m ∧B Moment on a dipole.

(2.72)

Figure 2.19: Elementary circuit for calculating magnetic force.

2.6.2 Force on an Elementary Magnetic Moment Circuit

Consider a plane rectangular circuit carrying current I having elementary area dxdy = dA. Regard this as a vector pointing in the z direction dA. The force on this current in a field B(r) is F such that

F_x

Idy [ B_z ( x + dx ) − B_z ( x ) ] = I dydx

∂B_z

∂x

(2.73)

F_y

− Idx [ B_z ( y + dy ) − B_z ( y ) ] = I dydx

∂B_z

∂y

(2.74)

F_z

− Idx [ B_y ( y + dy ) − B_y ( y ) ]−I dy [ B_x ( x + dx ) − B_x ( x )]

− I dxdy

⎡
⎣

∂B_x

∂x

∂B_y

∂y

⎤
⎦

= I dydx

∂B_z

∂z

(2.75)

(using ∇. B = 0). Hence, summarizing: F = I dydx ∇B_z. Now define m = I dA = I dydx ∧z and take it constant. Then clearly the force can be written

F = ∇( B. m )

(2.76)

or strictly ( ∇B) . m.

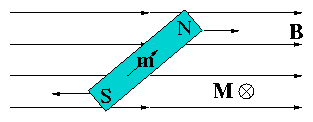
2.6.3 Example

Small bar magnet: archetype of dipole.

Figure 2.20: Moment on a bar magnet in a uniform field.

In uniform B feels just a torque aligning it with B. In a uniform field, no net force.

Non-uniform field: If magnet takes its natural resting direction, m parallel to B, force is

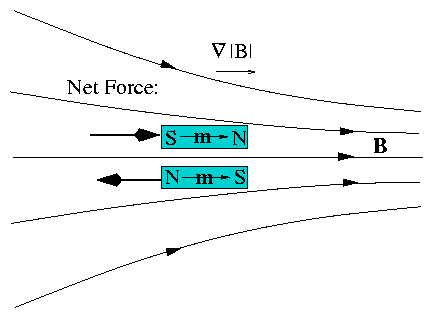
Figure 2.21: A magnetic moment in the form of a bar magnet is attracted or repelled toward the stronger field region, depending on its orientation.

F = m ∇|B|

(2.77)

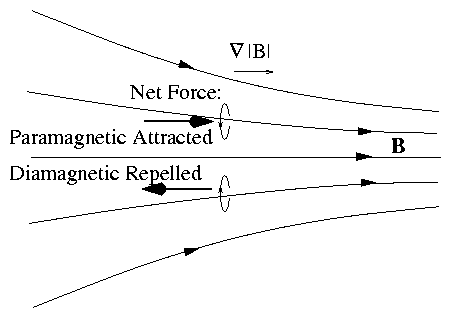
A bar magnet is attracted to high field. Alternatively if m parallel to minus B the magnet points other way

F = − m ∇|B| repelled from high |B|.

(2.78)

Same would be true for an elementary circuit dipole.

Figure 2.22: Elementary circuit acting as a dipole experiences a force in a non-uniform magnetic field.

It is attracted/repelled according to whether it acts to increase or decrease B locally. A charged particle moving in its Larmor orbit is always diamagnetic: repelled from high |B|.

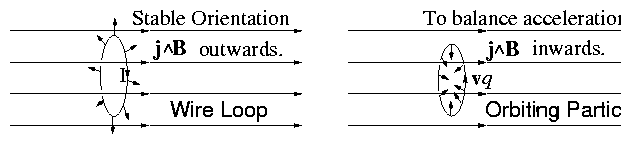
Figure 2.23: Difference between a wire loop and a particle orbit in their "natural" orientation.

2.6.4 Intuition

There is something slightly non-intuitive about the "natural" behavior of an elementary wire circuit and a particle orbit considered as similar to this elementary circuit. Their currents flow in opposite directions when the wire is in its stable orientation. The reason is that the strength of the wire sustains it against the outward magnetic expansion force, while the particle needs an inward force to cause the centripetal acceleration.

2.6.5 Angular Momentum

If the local current is made up of particles having a constant ratio of charge to mass: q/M say (Notational accident m is magnetic moment). Then the angular momentum is L = ∑_i M_i x_i ∧v and magnetic moment is m = ¹/₂ ∑q_i x_i ∧v_i. So

m =

L . "Classical"

(2.79)

This would also be true for a continuous body with constant (charge density)/(mass density) (ρ/ρ_m). Elementary particles, e.g. electrons etc., have `spin' with moments m, L. However they do not obey the above equation. Instead

m = g

(2.80)

with the Landé g-factor ( ≅ 2 for electrons). This is attributed to quantum and relativistic effects. However the "classical" value might not occur if ρ/ρ_m were not constant. So we should not be surprised that g is not exactly 1 for particles' spin.

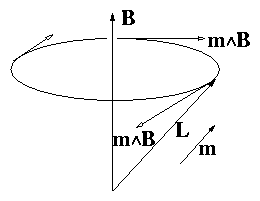
2.6.6 Precession of a Magnetic Dipole (formed from charged particle)

Figure 2.24: Precession of an angular momentum L and aligned magnetic moment m about the magnetic field.

The result of a torque m ∧B is a change in angular momentum. Since m = g Lq/2M we have

d L

= m ∧B= g

( L ∧B))

(2.81)

This is the equation of a circle around B. [Compare with orbit equation [(dv)/dt] = ^q/_m v∧B]. The direction of L precesses like a tilted `top' around direction of B with a frequency

ω = g

(2.82)

For an electron (g = 2) this is equal to the cyclotron frequency. For protons g = 2 ×2.79 [Written like this because spin is ¹/₂]. For neutrons g = 2 ×(−1.93).
Precession frequency is thus

f =

ω_electron

2 π

(28 GHz) ×(B/Tesla)

(2.83)

ω_proton

2π

(43 MHz) ×(B/Tesla)

(2.84)

This is the (classical) basis of Nuclear Magnetic Resonance but of course that really needs QM.

HEAD

Chapter 2 Particle Motion in Electric and Magnetic Fields

2.1 Electric Field Alone

2.2 Electrostatic Acceleration and Focussing

Examples:

Calculating focal length of aperture Radial acceleration.

2.2.1 Immersion Lens

2.2.2 Alternating Gradient Focussing

2.3 Uniform Magnetic field

2.3.1 Brute force solution:

2.3.2 `Physics' Solution

2.3.3 Relativistic Aside

2.3.4 Momentum Spectrometers

2.3.5 Historical Day Dream (J.J. Thomson 1897)

Electrostatic Deflection

Magnetic Deflection

2.3.6 Practical Spectrometer

2.4 Dynamic Accelerators

2.4.1 Cyclotron

2.4.2 Limitations of Cyclotron Acceleration: Relativity

2.4.3 Synchrotron

2.4.4 Linear Accelerators

2.5 Magnetic Quadrupole Focussing (Alternating Gradient)

2.5.1 Preliminary Mathematics

2.5.2 Multipole Expansion

2.6 Force on distributed current density

2.6.1 Forces on dipoles

Total force

Total Torque (Moment of force)

2.6.2 Force on an Elementary Magnetic Moment Circuit

2.6.3 Example

2.6.4 Intuition

2.6.5 Angular Momentum

2.6.6 Precession of a Magnetic Dipole (formed from charged particle)

Chapter 2
Particle Motion in Electric and Magnetic Fields