| HEAD | PREVIOUS |
Chapter 11
Monte Carlo Techniques
So far we have been focussing on how particle codes work once the
particles are launched. We've talked about how they are moved, and how
self-consistent forces on them are calculated. What we have not
addressed is how they are launched in an appropriate way in the first
place, and how particles are reinjected into a simulation. We've also
not explained how one decides statistically whether a collision has
taken place to any particle and how one would then decide what
scattering angle the collision corresponds to. All of this must be
determined in computational physics and engineering by the use of
random numbers and statistical distributions. Techniques based on random numbers
are called by the name of the famous casino at Monte Carlo.
11.1 Probability and Statistics
11.1.1 Probability and Probability Distribution
Probability, in the mathematically precise sense, is an idealization of the repetition of a measurement, or a sample, or some other test. The result in each individual case is supposed to be unpredictable to some extent, but the repeated tests show some average trends that it is the job of probability to represent. So, for example, the single toss of a coin gives an unpredictable result: heads or tails; but the repeated toss of a (fair) coin gives on average equal numbers of heads and tails. Probability theory describes that regularity by saying the probability of heads and tails is equal. Generally the probability of a particular class of outcomes (e.g. heads) is defined as the fraction of the outcomes, in a very large number of tests, that are in the particular class. For a fair coin toss, probability of heads is the fraction of outcomes of a large number of tosses that is heads, 0.5. For a six-sided die, the probability of getting any particular value, say 1, is the fraction of rolls that come up 1, in a very large number of tests. That will be one-sixth for a fair die. In all cases, because probability is defined as a fraction, the sum of probabilities of all possible outcomes must be unity. More usually, in describing physical systems we deal with a continuous real-valued outcome, such as the speed of a randomly chosen particle. In that case the probability is described by a "probability distribution" which is a function of the random variable (in this case velocity ). The probability of finding that the velocity lies in the range for small is then equal to . In order for the sum of all possible probabilities to be unity, we require11.1.2 Mean, Variance, Standard Deviation, and Standard Error
If we make a large number of individual measurements of a random value from a probability distribution , each of which gives a value , , then the sample mean value of the combined sample is defined as11.2 Computational random selection
Computers can generate pseudo-random numbers, usually by doing complicated non-linear arithmetic starting from a particular "seed" number (or strictly a seed "state" which might be multiple numbers). Each successive number produced is actually completely determined by the algorithm, but the sequence has the appearance of randomness, in that the values jump around in the range , with no apparent systematic trend to them. If the random number generator is a good generator, then successive values will not have statistically-detectable dependence on the prior values, and the distribution of values in the range will be uniform, representing a probability distribution Many languages and mathematical systems have library functions that return a random number. Not all such functions are "good" random number generators. (The built-in C functions are notoriously not good.) One should be wary for production work. It is also extremely useful, for example for program debugging, to be able to repeat a pseudo-random calculation, knowing the sequence of "random" numbers you get each time will be the same. What you must be careful about, though, is that if you want to improve the accuracy of a calculation by increasing the number of samples, it is essential that the samples be independent. Obviously, that means the random numbers you use must not be the same ones you already used. In other words, the seed must be different. This goes also for parallel computations. Different parallel processors should normally use different seeds. Now obviously if our computational task calls for a random number from a uniform distribution between 0 and 1, , then using one of the internal or external library functions is the way to go. However, usually we will be in a situation where the probability distribution we want to draw from is non-uniform, for example a Gaussian distribution, an exponential distribution, or some other function of value. How do we do that? We use two related random variables; call them and . Variable is going to be uniformly distributed between 0 and 1. (It is called a "uniform deviate".) Variable is going to be related to through some one-to-one functional relation. Now if we take a particular sample value drawn from the uniform deviate, , there is a corresponding value . What's more, we know that the fraction of drawn values that are in a particular -element , is equal to the fraction of values that are in the corresponding -element . Consequently, recognizing that those fractions are and respectively, where and are the respective probability distributions of and , we have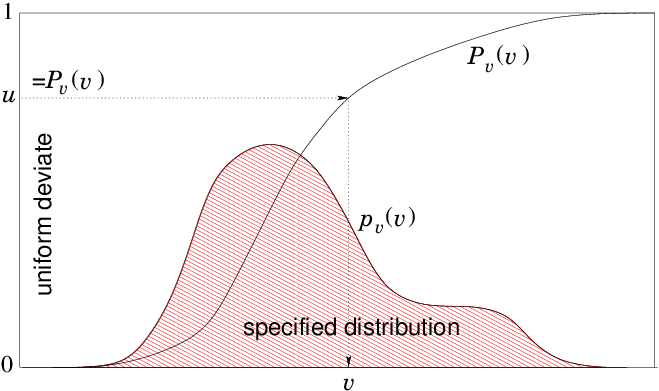
Figure 11.1: To obtain numerically a random variable with specified
probability distribution (not to scale), calculate a table
of the function by integration. Draw a random number from
uniform deviate . Find the for which by
interpolation. That's the random .
Since is monotonic, for any between 0 and 1, there is a
single root of the equation . Provided we can find that
root quickly, then given we can find . One way to make the root
finding quick is to generate a table of values of and ,
equally spaced in (not in ). Then given any , the
index of the point just below is the integer value *,
and we can interpolate between it and the next point using the
fractional value of *.
Rejection Method
Another way of obtaining random values from some specified probability
distribution is by the "Rejection Method", illustrated in Fig. 11.2. This involves using a second random number to decide
whether or not to retain the first one chosen. The second random
number is used to weight the probability of the first one.
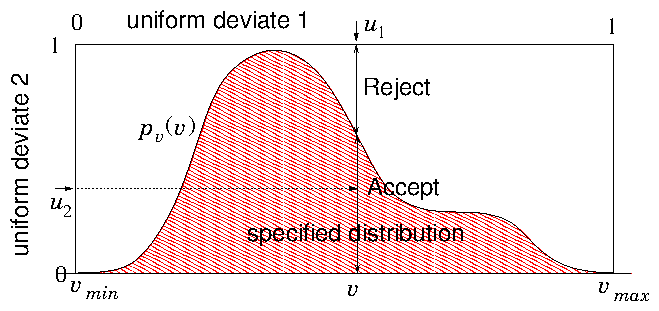
Figure 11.2: The rejection method chooses a value randomly from a
simple distribution (e.g. a constant) whose integral is
invertible. Then a second random number decides whether it will
be rejected or accepted. The fraction accepted at is equal
to the ratio of to the simple invertible distribution.
must be scaled by a constant factor to be everywhere
less than the simple distribution (1 here).
In effect this means picking points below the first scaled
distribution, in the illustrated case of a rectangular distribution,
uniformly distributed within the rectangle, and accepting only those
that are below (suitably scaled to be everywhere less than
1). Therefore some inefficiency is inevitable. If the area under
is, say, half the total, then twice as many total choices are
needed, and each requires two random numbers, giving four
times as many random numbers per
accepted point. Improvement on the second inefficiency can be obtained
by using a simply invertible function that fits more
closely. Even so, this will be slower than the tabulated function
method, unless the random number generator has very small cost.
Monte Carlo Integration Notice by the way, that this
second technique shows exactly how
"Monte Carlo Integration" can be done. Select points at random over
a line, or a rectangular area in two dimensions, or cuboid volume in
three dimensions. Decide whether each point is within the area/volume
of interest. If so, add the value of the function to be integrated to
the running total, if not, not. Repeat. At the end multiply the total
by the area/volume of the rectangle/cuboid divided by the number of
random points examined (total, not just those that are within the
area/volume). That's the integral. Such a technique can be quite an
efficient way, and certainly an easy-to-program way, to integrate over
a volume for which it is simple to decide whether you are inside it
but hard to define systematically where the boundaries are. An example
might be the volume inside a cube but outside a sphere placed
off-center inside the cube. The method's drawback is that its accuracy
increases only like the inverse square root of the number of
points sampled. So if high accuracy is required, other methods may be
much more efficient.
11.3 Flux integration and injection choice.
Suppose we are simulating a sub-volume that is embedded in a larger region. Particles move in and out of the sub-volume. Something interesting is being modelled within the subvolume, for example the interaction of some object with the particles. If the volume is big enough, the region outside the subvolume is relatively unaffected by the physics in the subvolume, then we know or can specify what the distribution function of particles is in the outer region, at the volume's boundaries. Assume that periodic boundary conditions are not appropriate, because, for example, they don't well represent an isolated interaction. How do we determine statistically what particles to inject into the subvolume across its boundary?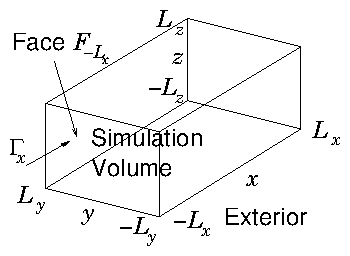
Figure 11.3: Simulating over a volume that is embedded in a wider
external region, we need to be able to decide how to inject
particles from the exterior into the simulation volume so as
to represent statistically the exterior distribution.
Suppose the volume is a cuboid shown in Fig. 11.3. It has 6
faces, each of which is normal to one of the coordinate axes, and
located at , or . We'll consider the face
perpendicular to which is at , so that positive velocity
corresponds to moving into the simulation sub-volume. We calculate
the rate at which particles are crossing the face into the
subvolume. If the distribution function is , then
the flux density in the direction is
Afterwards, we can normalize by dividing by , ariving at the cumulative flux weighted probability for . We then proceed as follows.
| 1. | Choose a random from its cumulative flux-weighted probability . |
| 2. | Choose a random from its cumulative probability for the already chosen , namely regarded as a function only of . |
| 3. | Choose a random from its cumulative probability for the already chosen and , namely regarded as a function only of . |
Naturally for other faces, and one has to start with the corresponding velocity component and cycle round the indices. For steady external conditions all the cumulative velocity probabilities need to be calculated only once, and then stored for subsequent time steps. Discrete particle representation An alternative to this continuum approach is to suppose that the external distribution function is represented by a perhaps large number, , (maybe millions) of representative "particles" distributed in accordance with the external velocity distribution function. Particle has velocity and the density of particles in phase space is proportional to the distribution function, that is to the probability distribution. Then if we wished to select randomly a velocity from the particle distribution we simply arrange the particles in order and pick one of them at random. However, when we want the particles to be flux-weighted, in normal direction say, we must select them with probability proportional to (when positive, and zero when negative). Therefore, for this normal direction we must consider each particle to have appropriate weight. We associate each particle with a real index so that when the particle is indicated. The interval length allocated to particle is chosen proportional to its weight, so that . Then the selection consists of a random number draw , multiplied by the total real index range and indexed to the particle and hence to its velocity: . The discreteness of the particle distribution will generally not be an important limitation for a process that already relies on random particle representation. The position of injection will anyway be selected differently even if a representative particle velocity is selected more than once.
Worked example: High Dimensionality Integration
Monte Carlo techniques are commonly used for high-dimensional problems; integration is perhaps the simplest example. The reasoning is approximately this. When there are dimensions, the total number of points in a grid whose size is in each coordinate-direction is . The fractional uncertainty in estimating a one-dimensional integral of a function with only isolated discontinuities, based upon evaluating it at grid points, may be estimated as . If this estimate still applies to multiple dimension integration (and this is the dubious part), then the fractional uncertainty is . By comparison, the uncertainty in a Monte-Carlo estimate of the integral based on evaluations is . When is larger than 2, the Monte Carlo square-root convergence scaling is better than the grid estimate. And if is very large, Monte Carlo is much better. Is this argument correct? Test it by obtaining the volume of a four-dimensional hypersphere by numerical integration, comparing a grid technique with Monte Carlo.A four-dimensional sphere of radius 1 consists of all those points for which . Its volume is known analytically; it is . Let us evaluate the volume numerically by examing the unit hypercube , . It is th of the hypercube , inside of which the hypersphere fits; so the volume of of the hypersphere that lies within the unit hypercube is th of its total volume; it is . We calculate this volume numerically by discrete integration as follows. A deterministic (non-random) integration of the volume consists of constructing an equally spaced lattice of points at the center of cells that fill the unit cube. If there are points per edge, then the lattice positions in the dimension () of the cell-centers are , where is the (dimension-) position index. We integrate the volume of the sphere by collecting values from every lattice point throughout the unit hypercube. A value is unity if the point lies within the hypersphere ; otherwise it is zero. We sum all values (zero or one) from every lattice point and obtain an integer equal to the number of lattice points inside the hypersphere. The total number of lattice points is equal to . That sum corresponds to the total volume of the hypercube, which is 1. Therefore the discrete estimate of the volume of th of the hypersphere is . We can compare this numerical integration with the analytic value and express the fractional error as the numerical value divided by the analytic value, minus one:
Monte Carlo integration works essentially exactly the same except that the points we choose are not a regular lattice, but rather they are random. Each one is found by taking four new uniform-variate values (between and ) for the four coordinate values . The point contributes unity if it has and zero otherwise. We obtain a different count . We'll choose to use a total number of random point positions exactly equal to the number of lattice points , although we could have made any integer we like. The Monte Carlo integration estimate of the volume is . I wrote a computer code to carry out these simple procedures, and compare the fractional errors for values of ranging from 1 to 100. The results are shown in Fig. 11.4.
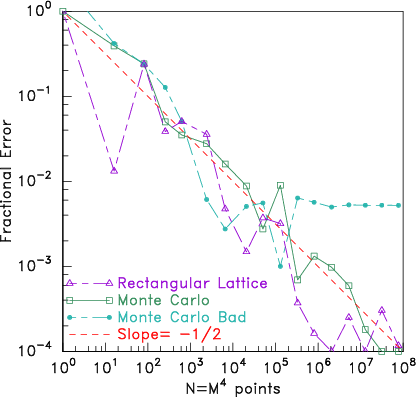
Figure 11.4: Comparing error in the volume of a hypersphere found
numerically using lattice and Monte Carlo integration. It turns out
that Monte Carlo integration actually does not
converge significantly faster than lattice integration, contrary to
common wisdom. They both converge approximately like
(logarithmic slope ). What's more, if one
uses a "bad" random number generator (the Monte Carlo Bad
line) it is possible the random integration will cease
converging at some number, because it gives only a finite-length
of independent random numbers, which in this case is exhausted
at roughly a million.
Four dimensional lattice integration
does as well as Monte Carlo for this sphere. Lattice
integration is not as bad as the dubious assumption of fractional
uncertainty suggests; it is more like
for . Only at higher dimensionality than do tests show the
advantages of Monte Carlo integration beginning to be significant.
As a bonus, this integration experiment detects poor random number
generators.
Exercise 11. Monte Carlo Techniques
1. A random variable is required, distributed on the interval with probability distribution , with a constant. A library routine is available that returns a uniform random variate (i.e. with uniform probability ). Give formulas and an algorithm to obtain the required randomly distributed value from the returned value.
2. Particles that have a Maxwellian distribution
3. Write a code to perform a Monto Carlo integration of the area under the curve for the interval . Experiment with different total numbers of sample points, and determine the area accurate to 0.2%, and approximately how many sample points are needed for that accuracy.
| HEAD | NEXT |